| | hhhh Impossible |  |
|
|
| Auteur | Message |
|---|
Emerson
Maître
 Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: hhhh Impossible Mar 23 Mar 2010, 21:07 | |
| H=1+1/2+1/3.....................1/n ktob H bdalalat n  | |
|
| | |
Othmaann
Expert grade1
Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
| | Sujet: Re: hhhh Impossible Mar 23 Mar 2010, 21:52 | |
| Il me semble que cest : 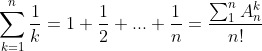 sauf erreur ... | |
|
| | |
SherlocK
Maître
Nombre de messages : 102
Age : 31
Localisation : Khouribga, Maroc
Date d'inscription : 22/11/2009
| | Sujet: Re: hhhh Impossible Mar 23 Mar 2010, 22:04 | |
| Existe-t-il une autre solution sans dénombrement (les suites par ex) ? | |
|
| | |
Othmaann
Expert grade1
Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
| | Sujet: Re: hhhh Impossible Mar 23 Mar 2010, 22:15 | |
| certainement ...
on peut facilement etudier cette suite montrer quelle est croissante , quelle est bornée et quelle est convergente ...!! mais pr l'ecriture generale je suis tjr a la recherche d'une solution! | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Mer 24 Mar 2010, 00:02 | |
| Ouai Bien sur ces 1er questions semblent trop facile mais j ai prposè cett qst par hasard pr savoir s kil est possible de trver lecrtre generale ou nn | |
|
| | |
codex00
Expert sup
Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
| | Sujet: Re: hhhh Impossible Mer 24 Mar 2010, 00:20 | |
| - Othmaann a écrit:
- certainement ...
on peut facilement etudier cette suite montrer quelle est croissante , quelle est bornée et quelle est onvergente ...!! mais pr l'ecriture generale je suis tjr a la recherche d'une solution! La suite harmonique Diverge (démontrable par définition de la limite) | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Mer 24 Mar 2010, 22:18 | |
| Et Comment on va la demontrer ? | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Mer 24 Mar 2010, 23:07 | |
| Sinon Mr.othman peux tu nous expliquer ta methode de denombrement (prsk on a po encore fait l cours)! | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Sam 27 Mar 2010, 21:48 | |
| | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Sam 27 Mar 2010, 21:56 | |
| ma reponse :je pense que puisque la suite n'est ni arithmetique ni géometrique ni recurrente Alors il n a aucune Forme-figure determinèè.Mais si cest possible la suite sera determinè par la formule de denombrement de mr Othmaane . | |
|
| | |
Bison_Fûté
Expert sup
Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
| | Sujet: Re: hhhh Impossible Sam 27 Mar 2010, 22:32 | |
| - Emerson a écrit:
- ma reponse :je pense que puisque la suite n'est ni arithmetique ni géometrique ni recurrente Alors il n a aucune Forme-figure determinèè.Mais si cest possible la suite sera determinè par la formule de denombrement de mr Othmaane .
BSR Emerson !! La suite que tu as proposée est une SUITE RECURRENTE . En effet , si on pose pour chaque entier naturel n ; n>=1 Un =1+(1/2)+(1/3)+ ...... + (1/n) alors ta suite est définie par la donnée de son 1er terme U1=1 et par la relation de récurrence suivante U(n+1)=Un+(1/(n+1) pour tout n>=1 . Et il n'y a que de cette manière qu'elle peut être présentée .... LHASSANE | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Sam 27 Mar 2010, 23:08 | |
| Merci a vous Mr Bison_Fûté
U(1)=U(0)+1 mais Qui ns a dit que U(0)=0? | |
|
| | |
Bison_Fûté
Expert sup
Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
| | Sujet: Re: hhhh Impossible Sam 27 Mar 2010, 23:12 | |
| BSR Emerson !!
J'ai écrit :
<< la relation de récurrence suivante
U(n+1)=Un+(1/(n+1) pour tout n>=1 >>
Donc la suite (Un)n est indexée sur IN* , en clair elle commence à partir de U1 .
LHASSANE | |
|
| | |
Emerson
Maître
Nombre de messages : 106
Age : 31
Localisation : khouribga
Date d'inscription : 24/11/2009
| | Sujet: Re: hhhh Impossible Sam 27 Mar 2010, 23:34 | |
| La suite doit etre indexer par n seulement et non Un donc U(n+1)=Un+(1/(n+1) est la seule forme-figure Qu on peuve ecrire.
Merci Bison_Fûté | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: hhhh Impossible | |
| |
|
| | |
| | hhhh Impossible | |
|
