|
| | arithmétique |  |
| | | Auteur | Message |
|---|
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: arithmétique Sujet: arithmétique  Sam 03 Avr 2010, 21:24 Sam 03 Avr 2010, 21:24 | |
| salam, a,b,c,d £ IN*, prouver que: ad=bc ===> a+ b + c + d n'est pas premier  | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 13:16 Lun 05 Avr 2010, 13:16 | |
| sans nuir a la géneralité du probléme supposons que :
a>=b>=c>=d
il clair que :
d/b et c/a
donc
d+c/a+b
alors : d+c/a+b+c+d
ce qui prouve que ce nombre n'est pas premier , sauf erreur bien sûr ^^ !! | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 13:52 Lun 05 Avr 2010, 13:52 | |
| - darkpseudo a écrit:
- sans nuir a la géneralité du probléme supposons que :
a>=b>=c>=d
il clair que :
d/b et c/a
donc
d+c/a+b
alors : d+c/a+b+c+d
ce qui prouve que ce nombre n'est pas premier , sauf erreur bien sûr ^^ !! non...pas forcément ... | |
|   | | majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 14:11 Lun 05 Avr 2010, 14:11 | |
| lemme(à prouver  ) : si ab=cd alors : \in%20\matbb%20N^{*}^{4}%20\right%20):a=xy%20\textbf{%20et%20}%20b=zt%20\textbf{%20et%20}c=xz%20\textbf{%20et%20}%20d=yt) ainsi a+b+c+d=xy+zt+xz+yt=(y+z)(x+t) conclure.... | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 18:11 Lun 05 Avr 2010, 18:11 | |
| Tu a raison et il y a une autre faute dans mon raisonnement ; pas fait attention ... | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 18:12 Lun 05 Avr 2010, 18:12 | |
| Remarquez juste que: a+b+c+d=[(a+b)(b+d)]/b | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 18:46 Lun 05 Avr 2010, 18:46 | |
| Mon idée s'apparente à celle de MohE. Jugez par vous-même. Solution complète :Posons, pour des besoins de concision : 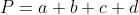 . +c(a+b)=(a+b)(a+c)) Ainsi, a divise (a+c)) , et donc, d'après le lemme d'Euclide, a divise (a+b) ou a divise (a+c), ou encore, a divise b ou a divise c. Par symétrie des rôles, étudions uniquement le cas où a divise b. %20+%20d(a+b)%20=%20(a+b)(b+d)) Semblablement, on peut déduire que b divise a, ou b divise d. - Si b divise a : Puisque a divise b, il vient que a=b (car encore, ce sont des entiers naturels) Et puisque ad=bc, et que les entiers ne sont pas nuls, il vient que d=c. Ainsi, P=a+b+c+d = a+a+c+c=2(a+c), qui est divisible par deux, et n'est donc pas premier. - Si b divise d : Puisque a divise b, et b divise d, il vient par transitivité que a divise d. Aussi, puisque b divise d, alors bc divise dc, ad divise dc, et donc, a divise c. Par suite, a divise a, b, c et d, et donc, a divise (a+b+c+d), a divise P. P est divisible par a, et n'est donc pas premier. En conclusion, P est toujours un nombre non premier. | |
|   | | MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 19:27 Lun 05 Avr 2010, 19:27 | |
| - Dijkschneier a écrit:
- Mon idée s'apparente à celle de MohE. Jugez par vous-même.
Solution complète :
Posons, pour des besoins de concision : 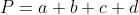 . .
+c(a+b)=(a+b)(a+c))
Ainsi, a divise (a+c)) , et donc, d'après le lemme d'Euclide, a divise (a+b) ou a divise (a+c), ou encore, a divise b ou a divise c. , et donc, d'après le lemme d'Euclide, a divise (a+b) ou a divise (a+c), ou encore, a divise b ou a divise c.
Par symétrie des rôles, étudions uniquement le cas où a divise b.
%20+%20d(a+b)%20=%20(a+b)(b+d))
Semblablement, on peut déduire que b divise a, ou b divise d.
- Si b divise a :
Puisque a divise b, il vient que a=b (car encore, ce sont des entiers naturels)
Et puisque ad=bc, et que les entiers ne sont pas nuls, il vient que d=c.
Ainsi, P=a+b+c+d = a+a+c+c=2(a+c), qui est divisible par deux, et n'est donc pas premier.
- Si b divise d :
Puisque a divise b, et b divise d, il vient par transitivité que a divise d.
Aussi, puisque b divise d, alors bc divise dc, ad divise dc, et donc, a divise c.
Par suite, a divise a, b, c et d, et donc, a divise (a+b+c+d), a divise P.
P est divisible par a, et n'est donc pas premier.
En conclusion, P est toujours un nombre non premier. Pour appliquer la lemme d'Euclid, il faut que PGCD(a+b,a+c)=1. | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Lun 05 Avr 2010, 21:22 Lun 05 Avr 2010, 21:22 | |
| - Dijkschneier a écrit:
- Mon idée s'apparente à celle de MohE. Jugez par vous-même.
Solution complète :
Posons, pour des besoins de concision : 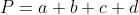 . .
+c(a+b)=(a+b)(a+c))
Ainsi, a divise (a+c)) , et donc, d'après le lemme d'Euclide, a divise (a+b) ou a divise (a+c), ou encore, a divise b ou a divise c. , et donc, d'après le lemme d'Euclide, a divise (a+b) ou a divise (a+c), ou encore, a divise b ou a divise c.
Par symétrie des rôles, étudions uniquement le cas où a divise b.
%20+%20d(a+b)%20=%20(a+b)(b+d))
Semblablement, on peut déduire que b divise a, ou b divise d.
- Si b divise a :
Puisque a divise b, il vient que a=b (car encore, ce sont des entiers naturels)
Et puisque ad=bc, et que les entiers ne sont pas nuls, il vient que d=c.
Ainsi, P=a+b+c+d = a+a+c+c=2(a+c), qui est divisible par deux, et n'est donc pas premier.
- Si b divise d :
Puisque a divise b, et b divise d, il vient par transitivité que a divise d.
Aussi, puisque b divise d, alors bc divise dc, ad divise dc, et donc, a divise c.
Par suite, a divise a, b, c et d, et donc, a divise (a+b+c+d), a divise P.
P est divisible par a, et n'est donc pas premier.
En conclusion, P est toujours un nombre non premier. Une question stp : 5*4=10*2 5+4+10+2 = 21 ce nombre n'est pas divisible par 2 et n'est pas divisible par un des nombres composant l'addition ... trouvez l'erreur ^^' | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Mar 06 Avr 2010, 13:19 Mar 06 Avr 2010, 13:19 | |
| - Citation :
- Pour appliquer la lemme d'Euclid, il faut que PGCD(a+b,a+c)=1.
Je ne pense pas. Tu confonds probablement avec le lemme de Gauss. - Citation :
- Une question stp : 5*4=10*2
5+4+10+2 = 21
ce nombre n'est pas divisible par 2 et n'est pas divisible par un des nombres composant l'addition ... trouvez l'erreur ^^' Merci de poser clairement la question. | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Mar 06 Avr 2010, 19:16 Mar 06 Avr 2010, 19:16 | |
| Voila ce que je voulais dire Dijkshneier :
D'aprés ma modeste comprehension de ta démonstration , le nombre a+b+c+d est divisible soit par 2 soit par a
or :
5*4 = 10 * 2 <==> ad=bc
mais : 5+4+10+2 = 21 et ce nombre n'est divisible ni par a ( tel que est 5 ou 4 ou 10 ou 2 ) ni par 2 ( c'est un peu lourd puisque je viens de le citer avant mais juste par souci de compréhension je le redis ) je conclu d'aprés ce contre-exemple que quelque chose cloche dans ta démonstration ... | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Mar 06 Avr 2010, 20:22 Mar 06 Avr 2010, 20:22 | |
| Voila une solution que je propose : ( remarque c'est presque celle que j'ai donner au début )
Tout d'abord il est impossible que ad=bc si tout ces nombres sont premiers entre eux :
on a : ad=bc peut alors aussi s'écrire sous la forme kcd=kdc
tel que d et c sont les nombre qui divisent respectivement b et a .
parceque supposons qu'aucun des nombre ne divisent l'autre et que a>=b>=c>=d
a=kb+r et c = nd+p
on aura ad=bc <==> (kb+r)d=(nd+p)b
kbd+rd=nbd+pb
k=n et r = p
ce qui nous donne a=nb+p et c = nd+p donc
a=qe et c=qt
ed=tb <==> b = ed/t
or t ne peut diviser e car si c'est le cas c diviserai a ce qui serait absurde d'aprés ce que nous avions supposer ...
et d'aprés la lemme de gausse t divise necessairement d donc
d=ty ( je commence a manquer de lettre XD )
et de même b = eh ... qety=qteh donc h=y
donc a+b+c+d=qe+eh+qt+ty
=qe+ey+qt+ty
=(q+y)(e+t) donc il n'est pas premier
revenons a nos moutons ^^ :
b=kd et a=kc
donc : a+b+c+d = (k+1)(d+c) qui n'est pas premier ce qui conclu les deux cas ^^ ...Sauf erreur ! | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  Jeu 08 Avr 2010, 19:09 Jeu 08 Avr 2010, 19:09 | |
| - darkpseudo a écrit:
- Voila ce que je voulais dire Dijkshneier :
D'aprés ma modeste comprehension de ta démonstration , le nombre a+b+c+d est divisible soit par 2 soit par a
or :
5*4 = 10 * 2 <==> ad=bc
mais : 5+4+10+2 = 21 et ce nombre n'est divisible ni par a ( tel que est 5 ou 4 ou 10 ou 2 ) ni par 2 ( c'est un peu lourd puisque je viens de le citer avant mais juste par souci de compréhension je le redis ) je conclu d'aprés ce contre-exemple que quelque chose cloche dans ta démonstration ... Merci pour ta repartie ; tu as raison, en effet. Et MoHe avait également raison, avant toi. Pour des entiers a,b et c arbitraires, a divise bc n'implique pas forcément que a divise b, ou a divise c. Mais si a est premier, on tombe alors sur le lemme d'Euclide, et la propriété est vérifiée. Merci pour vos remarques. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: arithmétique Sujet: Re: arithmétique  | |
| |
|   | | | | arithmétique |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
