imanos
Féru
 Nombre de messages : 66
Age : 30
Date d'inscription : 09/02/2010
 | | Sujet: 2 Inégalités (OWN) Ven 09 Avr 2010, 21:42 | |
| Bonsoir voici 2 OWN inéglalités la 1ere est tres facile 1ere inégalitéx,y,z>0 tels que x+y+z=3 MQ  2eme inégalitéa,b,c>0 et a+b+c=2 MQ  Bonne chance
Dernière édition par imanos le Sam 10 Avr 2010, 17:05, édité 1 fois | |
|
majdouline
Expert sup
Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: 2 Inégalités (OWN) Sam 10 Avr 2010, 14:17 | |
| oué la premiere est trop facile.. la deuxième aussi.... d'après Hölder on a :  et avec a+b+c=2   mais je me demande à quoi sert la condition: x+y=a ,x+z=b ,y+z=c??????!!!!  sauf erreur.... | |
|
Sylphaen
Expert sup
 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: 2 Inégalités (OWN) Sam 10 Avr 2010, 16:43 | |
| Voici pour la 1ér : Par Cs : 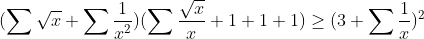 Il suffit de prouver donc que : 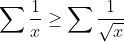 Ce qui esr vrai car : 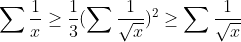 Puisque :  | |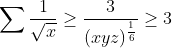
|
imanos
Féru
Nombre de messages : 66
Age : 30
Date d'inscription : 09/02/2010
| | Sujet: Re: 2 Inégalités (OWN) Sam 10 Avr 2010, 17:39 | |
| oué c Bon
pour les conditions j'ai confondu avec celles d'une autre iéngo que je posteré plus tard
sinn peu ton avoir une soluiton sans HOLDER? | |
|
MohE
Expert grade2
Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
| | Sujet: Re: 2 Inégalités (OWN) Sam 10 Avr 2010, 18:15 | |
| Belle inegos, mais je crois tout de même que la deuxième est plus facile que la première, vu que la deuxième a un point faible fatal, ma solution pour la première inégalité:
1/x² + 1/y² + 1/z² >= 2(1/x + 1/y + 1/z) -3
Il suffit donc de prouver que:
1/x + 1/y + 1/z + V(x)+V(y)+V(z)>=6
ce qui n'est qu'une application de Am-Gm deux fois. une autre methode consiste a utiliser le resultats de a²+b²>= 2ab, pour trouver qu'il suffit de prouver que:
1/V(x) + 1/V(y) + 1/V(z)>=3
après, on applique Jensen sur la fonction f(a)=1/V(a) qui est convexe, pour trouver le resultat voulu. | |
|
Contenu sponsorisé
| | Sujet: Re: 2 Inégalités (OWN) | |
| |
|
