NADIA
Féru
Nombre de messages : 49
Date d'inscription : 18/05/2006
 | | Sujet: Inégalités Lun 12 Avr 2010, 21:54 | |
| Bonsoir
j'ai une question est ce que: x^3<y équivaut à -y^(1/3) < x < y^(1/3) ?
Merci de votre aide | |
|
Othmaann
Expert grade1
 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
| | Sujet: Re: Inégalités Lun 12 Avr 2010, 22:30 | |
| sur R. NON sur [1;+linfini] oui | |
|
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Inégalités Mar 13 Avr 2010, 13:06 | |
| - NADIA a écrit:
- Bonsoir
j'ai une question est ce que: x^3<y équivaut à -y^(1/3) < x < y^(1/3) ?
Merci de votre aide 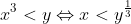 Sans l'autre côté, à ce que je sache, non ? D'ailleurs, on peut même généraliser, je pense : 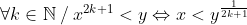 Mais bon, je ne suis pas du tout sûr. Quelqu'un confirmera peut-être. Au plaisir ! | |
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| |
Othmaann
Expert grade1
Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
| | Sujet: Re: Inégalités Mar 13 Avr 2010, 17:36 | |
| | |
|
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Inégalités Mar 13 Avr 2010, 18:45 | |
| - Dijkschneier a écrit:
- mizmaz a écrit:
- NADIA a écrit:
- Bonsoir
j'ai une question est ce que: x^3<y équivaut à -y^(1/3) < x < y^(1/3) ?
Merci de votre aide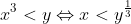
Sans l'autre côté, à ce que je sache, non ?
D'ailleurs, on peut même généraliser, je pense :
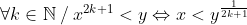
Mais bon, je ne suis pas du tout sûr. Quelqu'un confirmera peut-être.
Au plaisir ! C'est naturellement vrai dans 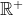 . Seulement, ce n'est pas toujours vrai lorsqu'on prend des nombres négatifs, car encore, on ne peut extraire la racine énième d'un nombre négatif. C'est vrai aussi pour 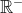 à mon avis. Considérons le polynôme P tel que =x^{2k+1}-a) avec 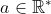 et 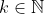 . Ma logique me dit que l'unique racine possible est 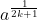 , le polynôme étant de degrés impair. L'identité remarquable dit que : =x^{2k+1}-a=(x-a^{\frac{1}{2k+1}})\sum_{i=0}^{2k}x^{2k-i}(a^{\frac{i}{2k+1}})) Considérons maintenant le polynôme F tel que : =\sum_{i=0}^{2k}x^{2k-i}(a^{\frac{i}{2k+1}})) Nous avons donc =(x-a^{\frac{1}{2k+1}})F(x)) Donc si F admet une racine, ce sera alors 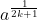Or, 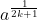n'est clairement pas une racine de F et donc F n'admet aucune racine réelle. Et puis F étant un polynôme de degrés pair et le coefficient de 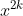 étant égal à 1 et donc positif, nous pouvons dire que =+\infty) Et donc que %3E0) et donc que le signe du polynôme P ne dépend que de 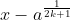 Déduisons finalement de là que : \in%20\mathbb{R}\;%20;\:%20\forall%20k\in%20\mathbb{N}\;%20/\;%20x^{2k+1}%3Ey\Leftrightarrow%20x%3Ey^{\frac{1}{2k+1}}) Sauf erreur, bien sûr. Au plaisir !  | |
|
