arithmetique

Habitué Nombre de messages : 29 Age : 30 Date d'inscription : 22/09/2009

on a/c et b/c et pgdc(a,b)=1
montrez que ab/c

bonne chance

c=ka / k appartient a Z
c=k'b / k' appartient a Z

ka=k'b => a/k'b =>(Gauss) a/k' [Vu que pgdc(a,b)=1]
et donc k'=pa / p appartient a Z

c=k'b=> c=pab => ab/c

slt , nous avons pas etudié arith mais je vas essayer :
on a c=ak (k£Z) , alors b divise ak .(car on a b/c)
pgcd(a,b)=1 ==> alors a et b sont premiers entre eux !
ce qui prouve que b divise k ==> k=bk' (k'£Z)
alors c=ak=abk' (k' £Z)
CQFD

Maître Nombre de messages : 234 Age : 31 Date d'inscription : 24/10/2009

Voici une démonstration qui manque probablement de pertinence. Mais bon.
Nous avons selon le théorème fondamental de l'arithmétique :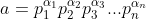
$arithmeti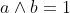que Gif.latex?a=p_{1}^{\alpha%20_{1}}p_{2}^{\alpha%20_{2}}p_{3}^{\alpha%20_{3}}..$
Et :
$arithmetique Gif.latex?b=p'_{1}^{\alpha'%20_{1}}p'_{2}^{\alpha'%20_{2}}p'_{3}^{\alpha'%20_{3}}..$
Puisque $arithmetique Gif$ alors : $arithmetique \;%20p_{i}\neq%20p'_{i'}$ (1)
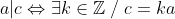Nous avons : $arithmetique \;%20c=ka$
Et :
$arithmetique \;%20c=k'b$
Donc :
$arithmetique Gif.latex?\left\{\begin{matrix}%20c=p_{1}^{\alpha%20_{1}}p_{2}^{\alpha%20_{2}}p_{3}^{\alpha%20_{3}}...p_{n}^{\alpha%20_{n}}k\\c=%20p'_{1}^{\alpha'%20_{1}}p'_{2}^{\alpha'%20_{2}}p'_{3}^{\alpha'%20_{3}}...p'_{n'}^{\alpha'%20_{n'}}k'%20\end{matrix}\right$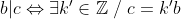
Et puisque (1) et puisque le théorème fondamental de l'arithmétique dit que chaque entier strictement positif peut être écrit comme un produit de nombres premiers d'une unique façon, à l'ordre près des facteurs, alors :
$arithmetique Gif.latex?c=p_{1}^{\alpha%20_{1}}p_{2}^{\alpha%20_{2}}p_{3}^{\alpha%20_{3}}...p_{n}^{\alpha%20_{n}}p'_{1}^{\alpha'%20_{1}}p'_{2}^{\alpha'%20_{2}}p'_{3}^{\alpha'%20_{3}}..$
Et par conséquent :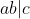
$arithmetique Gif$
CQFD
Sauf erreur.
Au plaisir ! Smile

PS : $arithmetique Gif.latex?(p_{1},p_{2},...,p_{n},p'_{1},p'_{2},..$ bien sûr. Smile

» SOS ARITHMETIQUE SVP
» arithmétique
» arithmetique
» arithmètique
» arithmétique