intégrale de la partie entiere

calculer l'intégrale de 0 jusqu'à 100 de E(x) dx et bonne chance

E(x) nest pas continue sur R , donc on ne peut prouver lexistence de cette integrale neanmois on peut poser cest integrale I et D'ESSAYER de le calculer :

I =

on a k<x<k+1(inégalités larges) alors on pose x = k+r tel que 0<=r<1
on prend r strictement inferieur a 1 ainsi le cas de k+1 sera dans le prochain integrale ...

donc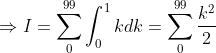


Sauf erreur...

c'est fausse !!
bcp des erreurs essayer de ne pas melanger les choses !! et merci

I= int(0;->n) E(x) dx = sum(k=0->n-1) int(k-> k+1){E(x) dx}

on sait que pr tt x£[k ; k+1] alors E(x) = k

donc int(k->k+1){E(x) dx} = k (k+1 - k) = k

donc I = sum(k=0->n-1) k = n(n-1)/2

alors pour n= 100 on aura :

I= 50*99=4950

et merci

Je ne vois pas ou est la faute , si jai fait un changement de variable ca devrait donner le meme resultat ...

Othmaann a écrit:

Je ne vois pas ou est la faute , si jai fait un changement de variable ca devrait donner le meme resultat ...

nn stp essayer d'être matheux!

si k£ IN on ne peux pas ecrire dk !!!!! et d'une part je sais est ce que tu veux utiliser x = [x] + {x} mais vrmt ce que tu as fais m'apparait plus logique
et merci

Othmaann a écrit:

Je ne vois pas ou est la faute , si jai fait un changement de variable ca devrait donner le meme resultat ...

Ton changement de variable est incorrect...
x = k + r donc dx = dr et non dk sur l'intervalle [k,k+1[...

Exactement ... J'aurais préféré avoir cette réponse dès le début!! Je m'excuse pr l'erreur.

la partie entière est définie sur des intervalles semi ouverts<k;k+1<donc pour intégrer sur un tel intervalle vous aurez affaire à une intégrale généralisée

salam


Voyons vous compliquez trop les choses

on est d'accord sur la relation de chasles

sur [k,k+1] , E(x) = constante = k , sauf pour k+1 ( point isolé)

integrale (k,k+1) de E(x) = lim [intg(k,t)de E(x)] quand t ----> (k+1)-

=lim k.(t-k) = k

donc :

intg(0,100) de E(x) = 0+1+2+........+99= 4950.

.

un peu de rigueur mathématique quand-même et merci