Exercices:

Je ne sais pas s'ils sont d'olympiades ou non, mais les voici:
1/Considérons ABCD un parallélogramme, et E un point de (AD) tel que EC=AB.
Montrez que le quadrilatère ABCE est inscriptible.
2/Soit C un cercle.
Considérons deux droites (D) et (D').
(D) coupe (C) en A et B.
(D') coupe (C) en E et F.
(D) et (D') se coupent en O.
O est au milieu de (C).
Sachant que AO=3 et OF=4 et OE=5.
Calculez BO.
3/Calculez A sachant que: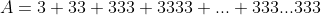
$Exercices: Gif.latex?A=3+33+333+3333+...+333..$ . (les trois se répètent n fois)
Bonne chance.

Expert grade2 Nombre de messages : 345 Age : 29 Date d'inscription : 28/01/2010

Il y a une faute dans le 2 exo???
OE=5 calculez OE??

slm exo 3 :
3+33+333+....+33....33 (n fois) = 1/3(9+99+....+99....99)(n fois)
Exercices: 1274817829412

Expert grade2 Nombre de messages : 345 Age : 29 Date d'inscription : 28/01/2010

Salut!
Pour le premier:
ABCD est un parallélogramme donc $Exercices: Gif$
On a (AB) $Exercices: Gif$ (DC) et (AE) les coupe donc $Exercices: Gif$
On remplaçant on a $Exercices: Gif$ (1)
AB=DC=EC donc (DCE) est isocèle en C d'ou :
$Exercices: Gif$
On remplace dans (1) et on a
$Exercices: Gif$
D'ou le quadrilatère ABCE et inscriptible.
Exercices: Icon_smile

Azerty1995 a écrit:: Il y a une faute dans le 2 exo???
OE=5 calculez OE??

Donc, il faut calculer BO.
C'est édité.

Expert grade2 Nombre de messages : 345 Age : 29 Date d'inscription : 28/01/2010

J'ai pas bien compris le 2 exo :
(D) et (D') se coupent en O le centre du cercle?

Azerty1995 a écrit:: J'ai pas bien compris le 2 exo :
(D) et (D') se coupent en O le centre du cercle?

Ils se coupent en un point au milieu du cercle.
Pas forcément O le milieu de ce cercle.

master a écrit:: slm exo 3 :
3+33+333+....+33....33 (n fois) = 1/3(9+99+....+99....99)(n fois)

Le raisonnement est juste mais n'ya-t-il pas de faute de calcul ???
Je n'ai pas compris d'ou vient le "n" , et la somme de ta suite geometrique ne m'a pas lair juste cest plutot
9.(10^n -1)/(10-1) = 10^n -1

Sauf erreur ...

Pour l'exercice de calcul:
On a 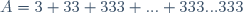$Exercices: Latex-1.tex?A=3+33+333+...+333..$ . (les trois se répètent n fois)
Donc 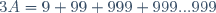$Exercices: Latex-1.tex?3A=9+99+999+999..$ . (les neufs se répètent n fois)
Donc $Exercices: Latex-1.tex?3A=10-1+100-1+1000-1+1000..$ . (les zéros se répètent n fois)
Donc $Exercices: Latex-1.tex?3A=10^1+10^2+10^3+10^n-1-1-1..$ . (les -1 se répètent n fois)
Donc $Exercices: Latex-1$ .
Posons $Exercices: Latex-1.tex?B=10^1+10^2+10^3+..$ et simplifions-le.
On a 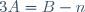$Exercices: Latex-1.tex?B=10^1+10^2+10^3+..$ .
Donc $Exercices: Latex-1.tex?10B=10^2+10^3+10^4+..$ .
Donc $Exercices: Latex-1.tex?10B-B=10^2+10^3+10^4+...+10^{n+1}-(10^1+10^2+10^3+..$ .
Donc $Exercices: Latex-1.tex?9B=10^2+10^3+10^4+...+10^{n+1}-10^1-10^2-10^3-..$ .
Donc $Exercices: Latex-1$ .
Donc $Exercices: Latex-1$ .
Donc $Exercices: Latex-1$ .
Donc $Exercices: Latex-1$ .
Donc $Exercices: Latex-1$ .
Donc $Exercices: Latex-1$ .
Ainsi la réponse master est fort juste.

@ othmaann : ma démo est juste , tu peux voire celle de nmo et tu vas trouver la meme reponse !, just dans la mienne j'ai évité les calcul en utilisant le sigma ! et je sais pas ce que ta pas compris !^^

Lol , non non excuse moi j'ai pas fait attention a quelque chose c'est bon merci.

nmo Pour la 11éme ligne: C'est plutot 9B=10^{n+1}+10^4-10-10^n BnC!!

nmo

Pour la 11éme ligne:
C'est plutot 9B=10^{n+1}+10^4-10-10^n

BnC!!

M.Marjani a écrit:: nmo
Pour la 11éme ligne:
C'est plutot 9B=10^{n+1}+10^4-10-10^n
BnC!!

J'ai oublié les points de suspensions.
Bonne remarque.
Maintenant c'est édité.

Deux autres exercices:
4/Montrez que $Exercices: Latex-1$ .
Sachant que a et b sont deux réels.
5/A est-il naturel?
$Exercices: Latex-1$ .
Bonne chance.
P.S: Il reste le deuxième exercice de la série en haut.

pour l'inégo est équivalente a :

Exercices: 1275304442352

donc il fallait montrer que a-b et a^3-b^3-a²+b²+a-b on eu la meme signe !

(*) si a-b>0 ==> a>b
on a :
Exercices: 1275304862830

puisque a>b ==> a(a²-a+1)>= b(b²-b+1)
avec meme !! on conclu cas 2 !

Si a²+b²+1>=a+b-ab
Donc
2a²+2b²+2-2a-2b+2ab>=0
Donc
(a+b-1)²+a²+b²>=0
Ce qui est vrai!
D'où le résultat.

Expert sup Nombre de messages : 1665 Age : 30 Date d'inscription : 05/03/2010

achraf_djy a écrit:: Si a²+b²+1>=a+b-ab
Donc
2a²+2b²+2-2a-2b+2ab>=0
Donc
(a+b-1)²+a²+b²>=0
Ce qui est vrai!
D'où le résultat.

Bien joué Achraf ! C'est ce que j'ai voullais écrire.
a²+b²+ab-(a+b)>=0
Multipliant par deux: 2(a²+b²)+2ab-2(a+b)>=0
<=> a²+b²+(a+b)²-2(a+b)>=0
a²-2a + b²-2b +(a+b)²>=0
a(a-2)+b(b-2)+(a+b)²>=0
Si: a>=2 et b>=2 ==> No probleme.
Si: a=<0 et b=<0 ==> No probléme.
--------------------------------------
Si: 0<a<2 et 0<b<2 => 2(a²+b²)+2ab-2(a+b)>=0.
Là j'ai pas osé de poster ^^.

Pour le deuxiéme:
A=(V2(V(47+21V5)/2+(2(7-3V5))/(7+3V5)(7-3V5)
= [V2(V47+21V5)-3V5+7]/2
On remarque que: 2 ne divise pas (V2(V47+21V5)-3V5+7).
A=[V2(V47+21V5)-3V5]/2+7/2
47 est un nombre premier <=> la valeur de V47 contient l'infini des chiffres aprés la virgule! <=> [V2(V47+21V5)-3V5] Contient l'inifini des chiffres aprés la virgule Ou bien [V2(V47+21V5)-3V5]£|N.
Vu que: 7/2=3.5, cela veut dire forcément que A contient au moins un chiffre aprés la virgule.
D'ou A n'appartient pas à |N.

J'attend vos remarques sur la methode.

M.Marjani a écrit:

achraf_djy a écrit:: Si a²+b²+1>=a+b-ab
Donc
2a²+2b²+2-2a-2b+2ab>=0
Donc
(a+b-1)²+a²+b²>=0
Ce qui est vrai!
D'où le résultat.

Bien joué Achraf ! C'est ce que j'ai voullais écrire.
a²+b²+ab-(a+b)>=0
Multipliant par deux: 2(a²+b²)+2ab-2(a+b)>=0
<=> a²+b²+(a+b)²-2(a+b)>=0
a²-2a + b²-2b +(a+b)²>=0
a(a-2)+b(b-2)+(a+b)²>=0
Si: a>=2 et b>=2 ==> No probleme.
Si: a=<0 et b=<0 ==> No probléme.
--------------------------------------
Si: 0<a<2 et 0<b<2 => 2(a²+b²)+2ab-2(a+b)>=0.
Là j'ai pas osé de poster ^^.
Pour le deuxiéme:
A=(V2(V(47+21V5)/2+(2(7-3V5))/(7+3V5)(7-3V5)
= [V2(V47+21V5)-3V5+7]/2
On remarque que: 2 ne divise pas (V2(V47+21V5)-3V5+7).
A=[V2(V47+21V5)-3V5]/2+7/2
47 est un nombre premier <=> la valeur de V47 contient l'infini des chiffres aprés la virgule! <=> [V2(V47+21V5)-3V5] Contient l'inifini des chiffres aprés la virgule Ou bien [V2(V47+21V5)-3V5]£|N.
Vu que: 7/2=3.5, cela veut dire forcément que A contient au moins un chiffre aprés la virgule.
D'ou A n'appartient pas à |N.
J'attend vos remarques sur la methode.

Pour le premier, il faut démontrer que a²+b²+1>=a+b-ab.
Et pas a²+b²>=a+b-ab comme tu as fait.
Pour le deuxième, il faut prouver que A est naturel.

Expert sup Nombre de messages : 1665 Age : 30 Date d'inscription : 05/03/2010

nmo a écrit:: Pour le premier, il faut démontrer que a²+b²+1>=a+b-ab.
Et pas a²+b²>=a+b-ab comme tu as fait.
Pour le deuxième, il faut prouver que A est naturel.

1/ Pour le premier EX j'adresse à Achref et je ne poste pas la réponse.
2/ Il m'apparait que A n'est pas naturel.. j'ai pas pris en considérance la racine.. Bon je re.

Expert sup Nombre de messages : 1665 Age : 30 Date d'inscription : 05/03/2010

Offre de revenche x)

On a: V47+21V5=(94+42V5)/2=(49+42V5+45)/2=(7+3V5)²/2
=> V(V47+21V5)=(7+3V5)/V2
=> V2*V(V47+21V5)=7+3V5
=> V2*V(V47+21V5)-3V5+7=(7+7)/2=7

CQFD.

M.Marjani a écrit:: Offre de revenche x)
On a: V47+21V5=(94+42V5)/2=(49+42V5+45)/2=(7+3V5)²/2
=> V(V47+21V5)=(7+3V5)/V2
=> V2*V(V47+21V5)=7+3V5
=> V2*V(V47+21V5)-3V5+7=(7+7)/2=7
CQFD.

Effectivement, c'est la bonne réponse.

nmo a écrit:: 2/Soit C un cercle.
Considérons deux droites (D) et (D').
(D) coupe (C) en A et B.
(D') coupe (C) en E et F.
(D) et (D') se coupent en O.
O est au milieu de (C).
Sachant que AO=3 et OF=4 et OE=5.
Calculez BO.

La figure,
Exercices: 1279343354_SS

Il est temps de répondre:
On a AOF=EOB. (angles)
Et BAF=BEF, car ce sont deux angles inscrits lmitant le même arc [BF].
Donc les deux triangles OAF et OEB sont semblables.
Donc les mesures de leurs côtés sont proportionnel.
Donc OA/OE=OF/OB.
Donc 3/5=4/OB.
Donc OB=4*5/3.
Donc OB=20/3.
Sauf erreur.

» exercices
» Exercices:
» Exercices du jeu exo par exo .
» DS 2 - 3 exercices
» EXERCICES C9