| | Encore les angles |  |
|
|
| Auteur | Message |
|---|
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Encore les angles Sujet: Encore les angles  Mer 09 Juin 2010, 15:56 Mer 09 Juin 2010, 15:56 | |
| EXO:
ABC est un triangle équilatéral.
[Bx) une demi droite coupe [AC] en D .
Sur [Bx) en dehors de [BD] , on marque un point E .
On suppose : l'angle CBD=20° , et AB = DE.
Déterminer : l'angle DEC ?
.............................................................. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Mer 09 Juin 2010, 16:46 Mer 09 Juin 2010, 16:46 | |
| Soit a la longueur commune des trois côtés du triangle ABC. D'après la loi des sinus dans le triangle DBC, il vient que  . Ensuite,  , d'où a) . Par souci de clarté, posons :  Dans le triangle BEC, le théorème d'Al-Kashi donne : a^2)  Pour finir, dans le même triangle BEC, la loi des sinus impose :  D'où :  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Mer 09 Juin 2010, 17:29 Mer 09 Juin 2010, 17:29 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Mer 09 Juin 2010, 17:40 Mer 09 Juin 2010, 17:40 | |
| Pragmatiquement, j'ai utilisé un moteur de calcul, je nomme : Wolfram Alpha.
Mais vous pouvez très bien réussir avec un calcul approché, à l'aide de votre calculatrice. Une fois sin(DEC) calculé approximativement, vous utilisez la fonction arcsin de votre calculatrice pour déduire la mesure approchée de l'angle DEC.
C'est bien l'inconvénient de l'approche trigonométrique : vous êtes englué dans un tas de calcul ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Jeu 10 Juin 2010, 09:59 Jeu 10 Juin 2010, 09:59 | |
| Je présente une autre solution:
Soit (D) une droite passant par B et parallèle à (AC).
Soit M le point d'intersection de (EC) et (D).
On a ABC un triangle équilatéral.
Donc ABC=ACB=BAC=60°. (angles)
On a DBC+ABD=ABC. (angles)
Donc 20°+ABD=60°. (angle)
Donc ABD=40°. (angle)
La somme des angles d'un triangle vaut 180°.
Dans le triangle ABD, on a ABD+ADB+BAD=180°. (angles)
Donc 40°+ADB+60°=180°. (angle)
Donc ADB+100°=180°. (angle)
Donc ADB=80°. (angle)
Soit K un point de [MB) et n'appartient pas à [BM].
On a KBA=BAC car ce sont deux angles échangés intérieurement limitées par les parallèles (D) et (AC) et leur interceptant (AB).
Donc ABK=60°. (angle)
On a ABK+ABC+CBM=180°. (angles)
Donc 60°+60°+CBM=180°. (angle)
Donc 120°+CBM=180°. (angle)
Donc CBM=60°. (angle)
Dans le quadrilatère ABMD, on a DAB+ABM=60°+ABC+CBM. (angles)
Donc DAB+ABM=60°+60°+60°. (angles)
Donc DAB+ABM=180°. (angles)
Donc le quadrilatère ABMD est un paralléllogramme.
Chaque angles juxtaposés de ce dernier sont égaux.
Alors BMD=DAB. (angles)
Donc BMD=60°. (angle)
On a aussi BCD=60°. (angle)
Donc le quadrilatère BMCD est inscriptible.
On a DBC et DMC deux angles qui interseptent le même arc DC.
Donc ils sont égaux.
Donc DMC=20°.==>(1) (angle)
On a ABMD est un paralléllogramme.
Donc AB=MD.
Et comme DE=AB.
Alors MD=DE.
Donc le triangle MDE est isocèle en D.
Donc DEM=DME. (angles)
Donc DEM=20°. (angle)
Donc DEC=20°. (angle)
Ainsi ma solution et celle de Dijkschneier ne convergent qu'en même sens.
Sauf erreur. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Jeu 10 Juin 2010, 10:25 Jeu 10 Juin 2010, 10:25 | |
| - nmo a écrit:
Donc DAB+ABM=180°. (angles)
Donc le quadrilatère ABMD est un paralléllogramme.
Une paire d'angles consécutifs supplémentaires ne suffit pas pour prouver qu'il s'agit d'un parallélogramme. Il vous faut au moins deux paires. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Jeu 10 Juin 2010, 10:39 Jeu 10 Juin 2010, 10:39 | |
| salam
Bravo à nmo et Dijkschneir pour le grand effort
.........................................
Une solution assez courte:
1)Sur [DE] , on marque un point F tel que : DFC isocèle en C.
2) Comparer les triangles : BDC et FCE
3) =====> DEC = 20°
................................................................................. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Jeu 10 Juin 2010, 11:06 Jeu 10 Juin 2010, 11:06 | |
| - houssa a écrit:
2) Comparer les triangles : BDC et FCE
De quelle sorte ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Jeu 10 Juin 2010, 11:10 Jeu 10 Juin 2010, 11:10 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Donc DAB+ABM=180°. (angles)
Donc le quadrilatère ABMD est un paralléllogramme.
Une paire d'angles consécutifs supplémentaires ne suffit pas pour prouver qu'il s'agit d'un parallélogramme. Il vous faut au moins deux paires. J'ajoute donc: Soit N un point appartenant à [BM), et qui n'appartient pas à [BM]. Posons MDC=a et BDC=b. On trouve facilemet que a+b=100°. On vérifie encore que DMN=b+80 et DMB=a. On a BMD+MDA=a+b+80°. Donc BMD+MDA=100°+80°. Donc BMD+MDA=180°. Et c'est la deuxième paire d'angle. Merci pour l'information que je ne connais pas. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Jeu 10 Juin 2010, 21:30 Jeu 10 Juin 2010, 21:30 | |
| Bien joué Dijksheiner, nmo, Mr houssam. Je propose cette methode: 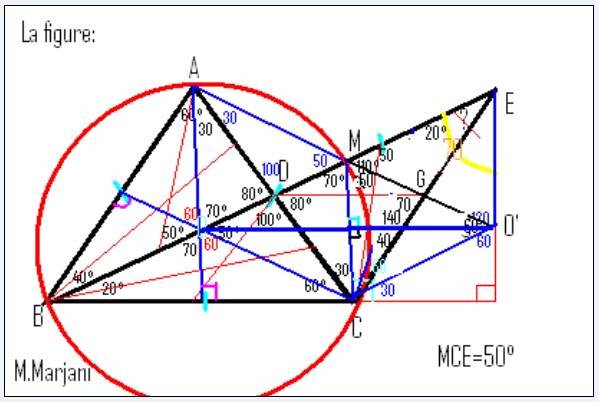 Quand j'aurais du temps je poste la methode écrite, mais je pense que la figure suffit de la comprendre. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Mer 30 Juin 2010, 11:59 Mer 30 Juin 2010, 11:59 | |
| - houssa a écrit:
- salam
Bravo à nmo et Dijkschneir pour le grand effort
.........................................
Une solution assez courte:
1)Sur [DE] , on marque un point F tel que : DFC isocèle en C.
2) Comparer les triangles : BDC et FCE
3) =====> DEC = 20°
................................................................................. Pour ma methode, il faut démontrer que ABMD est un paralléllogramme. Ce qui etait difficile pour moi, et il l'est maintenant. Pour comparer les deux triangles, je ne vois pas comment. Il serait gentil de la part de quelqu'un de m'aider. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  Mer 28 Juil 2010, 17:45 Mer 28 Juil 2010, 17:45 | |
| - houssa a écrit:
- salam
Bravo à nmo et Dijkschneir pour le grand effort
.........................................
Une solution assez courte:
1)Sur [DE] , on marque un point F tel que : DFC isocèle en C.
2) Comparer les triangles : BDC et FCE
3) =====> DEC = 20°
................................................................................. Je développe: On a ABC un triangle équilatéral. Donc ABC=ACB=CAB=60°. (angles) On a ABC=60°. (angle) Donc ABD+DBC=60°. (angles) Donc ABD+20°=60°. (angle) Donc ABD=40°. (angle) La somme des mesures d'un triangle vaut 180°. Dans le triangle ABD, on a ABD+DAB+BDA=180°. (angles) Donc 40°+60°+BDA=180°. (angle) Donc 100+BDA=180°. (angle) Donc BDA=80°. (angle) Et on a FDC=ADB car ce sont deux angles juxtaposé à tête. Donc FDC=80°. (angles) Et on a FDC=DFC car DFC est isocèle en C. Dans le triangle DFC, on a DFC+FDC+DCF=180°. (angles) Donc 80°+80°+DCF=180°. (angle) Donc 160°+DCF=180°. (angle) Donc DCF=20°. (angle) Et on a BCF=BCD+DCF. (angles) Donc BCF=60°+20°. (angle) Donc BCF=80°. (angle) Et puisque BFC=80°. (angle) Alors le triangle BFC est isocèle en B. Donc AC=BF. Donc AB=BF. Donc DE=BF. Donc DF+FE=BD+DF. Donc FE=BD.==>(1) Et on a DC=CF.==>(2) Et on a ADC=180°. (angle) Donc ADB+BDC=180°. (angle) Donc 80°+BDC=180°. (angles) Donc BDC=100°. (angle) Et de même EFC=100°. (angle) Donc EFC=CBD.==>(3) (angles) De 1, 2, et 3 on déduit que les deux triangles CEF et BDC sont isométriques. Donc les mesures de leurs angles juxtaposés sont égaux. Donc BEC=20°. (angle) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Encore les angles Sujet: Re: Encore les angles  | |
| |
|
  | |
| | Encore les angles |  |
|
