DISCUSSION du Grand jeu d'été 2010

cette discussion sera ouverte juska 16 h de demain
le Vainqueur du premier test est :
Dijkschneier
Félécitations !!

SYlphaen postera bientot les notes en détails!!

Expert sup Nombre de messages : 674 Age : 31 Date d'inscription : 28/06/2007

VOUS POUVEZ POSTEZ LES SOLUCES COMME 9A TOUT LE MONDE YSTAFD MAchi ghi les correcteurs.
amicalement.

OK on va essayer de poster une solution officielle (moi aussi je lui ai envoyé mes solutions ^^)

Bon Les voici :

Dijkschneier :Exo 1 : 7/7_ Exo 2 : 7/7 _Exo 3 : 1/7_ Exo 4 : 0/7
Total 15/28
Houssam110 : Exo 1 : 7/7_ Exo 2 : 7/7 _Exo 3 : 0/7_ Exo 4 : 0/7
Total 14/28
Darkpseudo : Exo 1 : 5/7_ Exo 2 : 1/7 _Exo 3 : 0/7_ Exo 4 : 0/7
Total : 6/7

Félicitation à Dijkschneier !

A toi de poster la nouvelle épreuve pour demain .
Je vois que le nombre de participant aujourd'hui est bien inférieur au nombre d'inscrit . J'espère que ca va augmenter ! DISCUSSION du Grand jeu d'été 2010 Icon_smile

& Bonne chance pour tous le monde ..

Expert sup Nombre de messages : 817 Age : 31 Date d'inscription : 31/10/2009

Bein merci , c'est vrai c'étais assez a la hauteur et j'ai bien aimé merci pour ce test , malheureusement demain je ne serai pas là donc a apré demain ; et bon jeu a tous

≠solutions proposées au premier test:
Exercice 1:
f(x)f(y)-f(x+y)=xy
pour x=y=0 f(0)=0 ou f(0)=1
si f(0)=0 pour y=0 on aura (∀x∈IR)f(x)=0 réciproquement ceci ne fonctionne pas!
ainsi f(0)=1 pour y=-x on a donc f(x)f(-x)=1-x²
pour x=1 f(1)=0 ou f(-1)=0
si f(1)=0...pour y=1 on a donc :-f(x+1)=x alors : (∀x∈IR)f(x)=1-x (1)
si f(-1)=0 ...pour y=-1 on a :-f(x-1)=-x : (∀x∈IR)alors f(x)=x+1 (2)
réciproquement (1) et (2) vérifient l'équation du départ :
conclusion : (∀x∈IR) f(x)=1-x ou f(x)=x+1
---------------------------------------------------------------------------------
Exercice 2:
notons : $DISCUSSION du Grand jeu d'été 2010 Gif$
l'inégalité est équivalente à :
$DISCUSSION du Grand jeu d'été 2010 Gif$
avec condition x+y+z=1 en levant au carré: l'inégalité est équivalente donc à:
$DISCUSSION du Grand jeu d'été 2010 Gif$
ce qui est clairement vrai avec Cauchy Schwartz!
-------------------------------------------------------------------------------------
Exercice 3:
notons : $DISCUSSION du Grand jeu d'été 2010 Gif.latex?n=d_{5}\times%20d_{i}%20\textit{%20avec%20}i\in%20\left%20\{%20\2,3,...$
et : $DISCUSSION du Grand jeu d'été 2010 Gif.latex?n=d_{6}\times%20d_{j}%20\textit{%20avec%20}j\in%20\left%20\{%20\2,3,...$
l'équation donnée est équivalente à :
$DISCUSSION du Grand jeu d'été 2010 Gif$
ce qui prouve par Bézout que : $DISCUSSION du Grand jeu d'été 2010 Gif$
ainsi $DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
si h≠1 ceci veut dire qu'il existe un diviseur de n entre d_{5} et d_{6} ce qui est impossible alors h=1 d'où:
$DISCUSSION du Grand jeu d'été 2010 Gif$
alors en revenant à du début on trouve que :
$DISCUSSION du Grand jeu d'été 2010 Gif$
alors les diviseurs de n sont :
$DISCUSSION du Grand jeu d'été 2010 Gif.latex?1%3C2%3Cd_{3}%3Cd_{4}%3Cd_{5}%3Cd_{6}=d_{5}+1%3C..$
supposons eu d_{5} et d_{6} sont composés alors on doit avoir au moins 4 diviseurs (fi3lia) inférieurs à d_{5} ce qui est impossible puisqu'on n'a que 3.
ainsi l'un des d_{5} ou d_{6} est premier (l'un est pair)!
si d_{5} est premier:
on a 4 cas :
$DISCUSSION du Grand jeu d'été 2010 Gif$
1)-si d_{6}=2d_{3}xd_{4} Or 2xd_{4} est aussi un diviseur ainsi 2xd_{4}>d_{6}=2d_{3}xd_{4} Or 2xd_{4}<=>d_{3}<1 contradiction
2)-si d_{6}=d_{3}xd_{4} Or d_{6} est pair alors d_{3} ou d_{4} est pair
si d_{3} est pair il soit donc forcément être 4 alors d_{6}=4d_{4} Or 2d_{4} est aussi un diviseur donc 2d_{4}>d_{6}=4d_{4}==>1>2 contradiction...mais si d_{4} est pair alors d_{4}=2d_{3} d'où d_{6}=4d_{3} alors 4 est un diviseurs de n .
alors d_{3}=4 d'où d_{6}=16 alors d_{5}=15 contradiction (15 n'est pas premier) ou d_{4}=4 alors d_{3}=3 d'où d_{6}=12 or 6 est aussi diviseur contradiction
3)-si d_{6}=2d_{4} Or 2d_{3} est aussi diviseurs qui est inférieur à:d_{6}=2d_{4} ainsi 2d_{3}=d_{4} alors d_{6}=4d_{3} alors 4 est un diviseurs de n :
alors d_{3}=4 d'où d_{6}=16 alors d_{5}=15 contradiction (15 n'est pas premier) ou d_{4}=4 alors d_{3}=3 d'où d_{6}=12 or 6 est aussi diviseur contradiction....
4)-si d_{6}=2d_{3} d_{4} est composé car sinon il doit être diviseur de d_{6} or seuls les deux diviseurs de d_{4} possible sont 2et d-{3} et on d_{4}<d_{6} alors d_{4}=4 d'où d_{3}=3 on revient donc à la discussion d'un cas déjà discuté est impossible
---------------------------------------------------------------------
ainsi d_{6} est le nombre premier :
d_{5} est composé ,on a de même 4 cas :
$DISCUSSION du Grand jeu d'été 2010 Gif$
si d_{5}=2xd_{3}xd_{4} Or 2d_{4} est aussi diviseur donc 2xd_{4}>d_{6}=2d_{3}xd_{4} Or 2xd_{4}<=>d_{3}<1 contradiction
2)-si d_{5}=d_{3}xd_{4} Or d_{5} est pair alors d_{3} ou d_{4} est pair
si d_{3} est pair il soit donc forcément être 4 alors d_{5}=4d_{4} Or 2d_{4} est aussi un diviseur donc 2d_{4}>d_{5}=4d_{4}==>1>2 contradiction...mais si d_{4} est pair alors d_{4}=2d_{3} d'où d_{5}=4d_{3} alors 4 est un diviseurs de n .
3)-si d_{5}=2d_{3} ,d_{4} est donc composé car sinon il doit être diviseur de d_{5} or seuls les deux diviseurs de d_{4} possible sont 2et d_{3} et on a d_{4}<d_{5} alors d_{4}=4 d'où d_{3}=3
alors d_{5}=6 d'où d_{6}=7 n=6x7=42 contraction car 4 est diviseur de n (4 ne divise pas 42)
4)-il nous reste le dernier cas d_{5}=2d_{4} Or 2d_{3} est aussi diviseurs qui est inférieur à:d_{5}=2d_{4} ainsi 2d_{3}=d_{4} alors d_{5}=4d_{3} alors 4 est un diviseurs de n :
alors d_{4}=4 d'où d_{3}=3 d'où d_{5}=8 donc d_{6}=9 qui n'est pas premier contradiction....ou bien d_{3}=4 d'où d_{4}=8 ==>d_{5}=16
alors d_{6}=17 d'où la solution
n=16x17=272

Bravo !!

houssam110 a écrit:: Bravo !!
regarde ceci il peu rendre ta solution plus courte
2d_5.d_6=d_5²+d_5²-1==> d_6-d_5=1

merci houssam ^^mais c'est deja cité dans ma solution... cherche!!je sais que c'est long xD

oh désolé

Expert sup Nombre de messages : 1482 Age : 30 Date d'inscription : 12/12/2009

Très joli, majdouline.

Bonjour! je m'excuse de ne pas être à temps pour proposer mes solutions, mais bon! voila ce que j'ai trouvé:
Solution du Problème 1:
si y=0 on trouver que f(x)=f(x).f(0) <=> f(x)=0 pour tous x ou f(0)=1, puisque le premier choix ne menne que vers l'absurde, il ne nous reste que le deuxième choix: f(0)=1.
si y=-x on aurra f(0)=f(x).f(-x)+x² => f(x).f(-x)=1-x².
si x=1 => f(1).f(-1)=0 => f(1)=0 ou f(-1)=0
cas 1: y=1 => f(x+1)=f(1).f(x)-x=-x => f(x)=1-x
cas 2: y=-1 => f(x)=1+x
Solution du Problème 2:
On note que ab+bc+ca=abc.
L'inégalité équivaut à:
\sum V(ab+c)-V(c) >= V(abc)
<=> \sum ab/[V(c)+V(ab+c)]>=V(abc)
<=> \sum abVc/[c+V(a+c)(b+c)]>=Vabc
<=> \sum V(ab)/[c+V(a+c)(b+c)]>=1
puisuqe 1/a + 1/b + 1/c=1 il doit exister trois réels positifs x,y et z tels que: a=p/x , b=p/y et c=p/z où p=x+y+z. après cette substitution, il nous faut prouver que:
\sum z/[V(xy)+V(x+z)(y+z)]>=1
or on sait déjà que V(xy) =< (x+y)/2 et V(x+z)(y+z)=<z+(x+y)/2 on sommant ces deux et en remplacant des l'inégalité précédante en trouve ce qu'il fallait démontrer, avec égalité si et seulement si a=b=c=3.
Solution du Problème 3:
k est le nombre des diviseures de n.
supposons que k>=12, alors d_6=<Vn et d_5<n => d_6²+d_5²<2n absurde, d'ou k<12, supposons encore que k<10 alors d_5>=Vn et d_6>=Vn+1 => d_5²+d_6²-1>=2n+2Vn>2n. ce qui est encore absurde, d'où k=10 ou k=11. si k=11 alors n est de la forme de p^10 avec p premier, ce qui implique que d_5=p^4 et d_6=p^5. l'equation prouve donc que: 2p^10=p^8+p^10-1 absurde, d'où k=10.
ainsi d_5*d_6=n en remplacants dans l'equation, on trouve que d_6=d_5+1 => 2|n. puisque k=10, on doit avoire n=p^9 ou n=p^4q avec p et q des nombres premiers. si n=p^9 alors n=2^9, or celle-ci ne vérifie pas l'équation. d'ou n=p^4q, cette dernière nous mène à deux cas: soit n=2^4p soit n=2p^4. Le deuxième cas implique que d_5=p^2 et d_6=2p^2. l'équation donc implique que p^4=1 ce qui est absurde. et ainsi n=2^4p=16p. on a d_6=d_5+1 donc l'un et seulement l'un deux parmi tout les diviseurs de n est impaire, ainsi p=d_6 ou p=d_5.
si d_5=p alors d_2=2,d_3=4,d_4=8, et d_6=16 =>p+1=16 => p=15 absurde, d'ou d_6=p par le même raisonement on trouve que p=17,et ainsi n=16*17=272.

Exo 4 :

ça peut prendre du temps à la comprendre. mais bon, j'avais bien essayer d'éclairer !
résumé: BCG= BCF <=> CFE=DCG
et puis j'avais démontré CFE=DCG

DISCUSSION du Grand jeu d'été 2010 127162Exo

DISCUSSION du Grand jeu d'été 2010 127162Exo

bonsoir soufiane Wink

ton raisonnement est faux ..... c'est vrai (ce que tu as écrit dans les 3 premières lignes)
si on veut démontrer P et on trouve que P<=>Q il suffit donc de prouver Q...
mais dans ton raisonnement t'as prouvé que :BCG= BCF <=> CFE=DCG
mais lorsque tu voulais prouver que CFE=DCG tu as utilisé le fait que BCG= BCF comme si c'est un donné or c'est ce qu'on cherche plutôt à prouver!

Je suis d'accord avec majdouline, en tout cas Soufiane, tu as fais u grand travail en essayant un exo de geométri, juste ton raisonement pour prouver que BCG= BCF <=> CFE=DCG est assez long, tant que cette dernière est faisable en deux ligne.

Indice: prouver dans la figure réalisé par soufiane et en utilisant Thalèse que les triangles FCD' et CGD sont semblables.

désolé j'ai pas fais attention !!

1.GDC=FD'C ( (BD)ll(FD') )
2.- \frac{GD}{D'C} = \frac{GD}{D'E} = \frac{AD}{AD'}
- \frac{DC}{D'F}=\frac{DB}{D'F}=\frac{AD}{AD'}
alors \frac{DG}{D'C}=\frac{DC}{D'F}

de 1 et 2 => les triangles FCD' et CGD sont semblables. (un angle égal compris entre deux côtés proportionnels)
<=> CFE=DCG et enfin BCG= BCF

merci Majdo. et Mohe Smile

solutions proposées au deuxième test:
Exercice1:
en prenant la deuxième équation:
y²+y(x-1)+x²=0 alors delta1=-3x²-2x+1 alors pour que le système ait une solution 3x²+2x-1≤0 alors 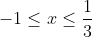$DISCUSSION du Grand jeu d'été 2010 Gif$
alors si -1<x≤0 alors x³≤0 et x²<1==>x³+x²<1 contradiction
si 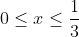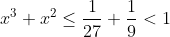$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$ contradiction
et puis x=1 ne vérifie aussi pas l'équation
ainsi S={ma localisation}
-------------------------------------------------------------------------------
Exercice2:
f(x+yf(x))+f(xf(y)-y)=f(x)-f(y)-2xy (1)
pour x=y=0 on aura :f(0)=0
pour x=0 on aura:f(-y)=-f(y)
en remplaçant y par -y
f(x-yf(x))+f(y-xf(y))=f(x)+f(y)-2xy
<=>f(x-yf(x))-f(xf(y)-y)=f(x)+f(y)-2xy (2)
en sommant (1) et (2) on a donc:
f(x+yf(x))+f(x-yf(x))=2f(x)
alors on pose x+yf(x)=a et x-yf(x)=b ...et ça devient:
$DISCUSSION du Grand jeu d'été 2010 Gif$
pour b=0 on aura:
$DISCUSSION du Grand jeu d'été 2010 Gif$
alors * devient:
$DISCUSSION du Grand jeu d'été 2010 Gif$
pour la relation (1) pour x=y
on aura : f(x+xf(x))+f(xf(x)-x)=2x² (3)
alors f(2xf(x))=2x²<=>f(xf(x))=x² (car f(2a)=2f(a))
ainsi si f(x)=0 ===> x=0
démontrons l'injection:
pour f(a)=f(b)<=>f(a)+f(-b)=0<=>f(a-b)=0==>a-b=0<=>a=b ce qui montre l'injection....
en revenant à (1= pour x=y=1 on aura :
f(1+f(1))=1+f(1) et pour x=-y=1 on aura : f(1-f(1))=f(1)-1 (par injection au moins l'un des f(1)-1 et f(1)+1 est different de 0..
1)-si f(1)+1=c est diffèrent de 0
de (1) on a : et en utilisant le résultat** on aura :
f(xf(y))+f(yf(x))=2xy
pour x=1 et y=c=f(1)+1 (f(c)=c)on a :
c+f(cf(1))=2c<=>f(cf(1))=f(c)==>f(1)=1
en revenant à (1) et pour x=1 on a :
f(1+y)+f(f(y)-y)=1-f(y)+2y
<=>f(f(y)-y))=-2f(y)+2y
alors notons m=f(y)-y (for all y £IR)
ça devient f(m)=-2m
et on a f(xf(x))=x² alors f(2m²)=-m²
on a : f(f(y)-y))=-2f(y)+2y
pour y=2m² ça devient:
f(-m²-2m²)=2m²+4m²
<=>f(-3m²)=6m²<=>f(m²)=-2m²<=>f(2m²)=-4m² Or on a f(2m²)=-m²
alors -4m²=-m² <=>m=0 d'où f(x)=x (for all x £IR)
2)-si f(1)-1=c' est diffèrent de 0
(on procède de la même manière pour prouver que f(x)=-x)
on a :f(xf(y))+f(yf(x))=2xy
pour x=1 et y=c' (f(c')=-c')
f(c'f(1))=c'=f(-c')==>f(1)=-1
en revenant à (1) pour y=1 on a donc:
f(x+f(x))+f(-x-1)=f(x)-f(1)+2x<=>f(x+f(x))=2f(x)+2x
notons x+f(x)=m' alors f(m')=2m'
et on a f(xf(x))=x² alors f(2m'²)=m'²
on a :f(x+f(x))=2f(x)+2x
pour x=2m'² : f(2m'²+m'²)=2m'²+4m'²<=>f(2m'²)=4m'² et on a f(2m'²)=m'² alors m'²=4m'² d'où m=0
alors (for all x£IR):f(x)=-x
réciproquement les deux solutions vérifient l'équation du départ!
conclusion :
$DISCUSSION du Grand jeu d'été 2010 Gif$
-------------------------------------------------------------------------------------
Exercice 3:
par homogénéité supposons que abc=1 l'inégalité est donc équivalente à: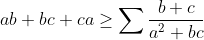
$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
$DISCUSSION du Grand jeu d'été 2010 Gif$
ce qui est clairement vrai!

Maître Nombre de messages : 152 Age : 31 Date d'inscription : 21/03/2009

salut majdouline
donc pr l'exo 2
a ta place on arrivant au stade de "ce qui est l'équation de Cauchy qui a pour solution f(x)=f(1)x "
j'aurai fais :
on pose f(1) =k
alors f(x) =kx pr tt x£R
et je revient faire reciproquement
ce qui donnera :
k(x+kxy)+k(kxy-y)=kx-ky-2xy
ce qui donne on supposant que x/=0 et y/=0 ; k^2=-1
et k£R !

Expert sup Nombre de messages : 1482 Age : 30 Date d'inscription : 12/12/2009

majdouline a écrit:: alors * devient:
$DISCUSSION du Grand jeu d'été 2010 Gif$
ce qui est l'équation de Cauchy qui a pour solution f(x)=f(1)x

Sans argument de continuité ou de monotonie, vous ne pouvez pas dire nécessairement que f(x)=f(1)x. Cf. les cas pathologiques de l'équation fonctionnelle de Cauchy.

tu as absolument raison Dijkschneier...je viens d'éditer...c'est un peu long xD

Avec le résultat f(a)+f(b)=2f((a+b)/2) je pense qu'on peut utiliser Jensen pour montrer que f ne peut être ni convexe ni concave sur aucun intervalle de IR donc il doit être affine ..

Sylphaen a écrit:: Avec le résultat f(a)+f(b)=2f((a+b)/2) je pense qu'on peut utiliser Jensen pour montrer que f ne peut être ni convexe ni concave sur aucun intervalle de IR donc il doit être affine ..

la continuité reste une condition nécessaire pour une telle conclusion...Or on n' a pas cette donnée là ....

Expert sup Nombre de messages : 1482 Age : 30 Date d'inscription : 12/12/2009

Sylphaen a écrit:: Avec le résultat f(a)+f(b)=2f((a+b)/2) je pense qu'on peut utiliser Jensen pour montrer que f ne peut être ni convexe ni concave sur aucun intervalle de IR donc il doit être affine ..

Il vous faut tout de même que f soit continue sur $DISCUSSION du Grand jeu d'été 2010 Gif$ pour aborder les choses ainsi. Et il ne s'agit pas de l'inégalité de Jensen, il s'agit d'une caractérisation des fonctions convexes.
Je vous rappelle la propriété :

Wikipédia a écrit:: Une fonction f continue sur I est convexe sur I si et seulement si quels que soient les éléments x1 et x2 de I :
$DISCUSSION du Grand jeu d'été 2010 Gif$

Ainsi, sous réserve d'une hypothétique continuité de f sur $DISCUSSION du Grand jeu d'été 2010 Gif$ , f serait à la fois convexe et concave, et donc affine.

» Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)
» c'est un grand grand grand défi
» Discussion
» pour étudier à NASA
» Discussion et Olympiade: