| | Facile, mais pas futile. |  |
|
|
| Auteur | Message |
|---|
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Facile, mais pas futile. Sujet: Facile, mais pas futile.  Sam 07 Aoû 2010, 21:58 Sam 07 Aoû 2010, 21:58 | |
| Soit  , prouver que:  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Sam 07 Aoû 2010, 22:44 Sam 07 Aoû 2010, 22:44 | |
| Facile par une AM-GM  a^3+b^3+c^3>=3abc , Or (a,b,c)>0, ab+bc+ac>=a²+b²+c² donc (a+b+c)²>=3(a²+b²+c²) D'ou le résultat. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Sam 07 Aoû 2010, 22:50 Sam 07 Aoû 2010, 22:50 | |
| - M.Marjani a écrit:
- Or (a,b,c)>0, ab+bc+ac>=a²+b²+c² donc (a+b+c)²>=3(a²+b²+c²)
Faux !! C'est l'inégalité inversée qui est vraie : a²+b²+c² >= ab+ac+bc. De même pour celle qui en découle. | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Sam 07 Aoû 2010, 22:56 Sam 07 Aoû 2010, 22:56 | |
| - M.Marjani a écrit:
- Facile par une AM-GM

a^3+b^3+c^3>=3abc , Or (a,b,c)>0, ab+bc+ac>=a²+b²+c² donc (a+b+c)²>=3(a²+b²+c²)
D'ou le résultat. J'ai dis facile, mais pas à ce point-là, car ça serait trivial sinon. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Sam 07 Aoû 2010, 22:58 Sam 07 Aoû 2010, 22:58 | |
| - Dijkschneier a écrit:
- M.Marjani a écrit:
- Or (a,b,c)>0, ab+bc+ac>=a²+b²+c² donc (a+b+c)²>=3(a²+b²+c²)
Faux !! C'est l'inégalité inversée qui est vraie : a²+b²+c² >= ab+ac+bc. De même pour celle qui en découle. Oui, t'as raison. 'I'm confused today!' | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Sam 07 Aoû 2010, 23:23 Sam 07 Aoû 2010, 23:23 | |
| - M.Marjani a écrit:
- Dijkschneier a écrit:
- M.Marjani a écrit:
- Or (a,b,c)>0, ab+bc+ac>=a²+b²+c² donc (a+b+c)²>=3(a²+b²+c²)
Faux !! C'est l'inégalité inversée qui est vraie : a²+b²+c² >= ab+ac+bc. De même pour celle qui en découle.
Oui, t'as raison. 'I'm confused today!' Je corrige: (a+b+c)²=(a+b+c)(a+b+c)>=9(abc)^{2/3} (a²+b²+c²)>=3(abc)^{2/3} (a+b+c)²/(a²+b²+c²)>=3 Le résultat découle.. | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 | |
  | |
personne
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 32
Date d'inscription : 28/08/2008
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 00:44 Dim 08 Aoû 2010, 00:44 | |
| salut 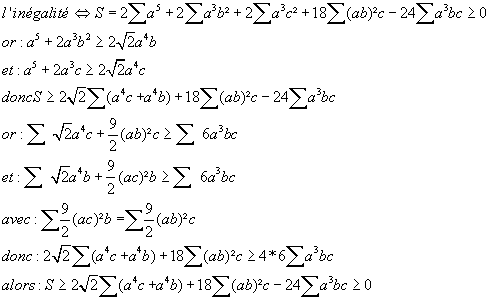 | |
|
  | |
personne
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 32
Date d'inscription : 28/08/2008
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 00:51 Dim 08 Aoû 2010, 00:51 | |
| - M.Marjani a écrit:
- M.Marjani a écrit:
- Dijkschneier a écrit:
- M.Marjani a écrit:
- Or (a,b,c)>0, ab+bc+ac>=a²+b²+c² donc (a+b+c)²>=3(a²+b²+c²)
Faux !! C'est l'inégalité inversée qui est vraie : a²+b²+c² >= ab+ac+bc. De même pour celle qui en découle.
Oui, t'as raison. 'I'm confused today!'
Je corrige:
(a+b+c)²=(a+b+c)(a+b+c)>=9(abc)^{2/3}
(a²+b²+c²)>=3(abc)^{2/3}
(a+b+c)²/(a²+b²+c²)>=3
Le résultat découle.. salut M Marjani ce qui est en rouge est faux | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 09:57 Dim 08 Aoû 2010, 09:57 | |
| - oussama1305 a écrit:
- Soit
 , prouver que: , prouver que:
 L'inégalité étant homogène, on peut normaliser le problème en supposant, sans perte de généralité, que abc = 1/3. On a d'après l'inégalité de Chebyschev : a^3+b^3+c^3 >= (a+b+c)(a²+b²+c²)/3, et d'après l'IAG : a+b+c >= 3(1/3)^(1/3) Par conséquent, LHS >= 2(a+b+c)(a²+b²+c²) + 9(a+b+c)²/(a²+b²+c²) >= 3(1/3)^(1/3) * (2x + 3(1/3)^(1/3)/x ) >= 33, où x = a²+b²+c². La dernière inégalité est vraie lorsque x>0, ce qui est le cas. | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 14:12 Dim 08 Aoû 2010, 14:12 | |
| - Dijkschneier a écrit:
- oussama1305 a écrit:
- Soit
 , prouver que: , prouver que:
 L'inégalité étant homogène, on peut normaliser le problème en supposant, sans perte de généralité, que abc = 1/3.
On a d'après l'inégalité de Chebyschev : a^3+b^3+c^3 >= (a+b+c)(a²+b²+c²)/3, et d'après l'IAG : a+b+c >= 3(1/3)^(1/3)
Par conséquent, LHS >= 2(a+b+c)(a²+b²+c²) + 9(a+b+c)²/(a²+b²+c²) >= 3(1/3)^(1/3) * (2x + 3(1/3)^(1/3)/x ) >= 33, où x = a²+b²+c².
La dernière inégalité est vraie lorsque x>0, ce qui est le cas.
Prends x = 3^{1/3}, qui est le cas d'égalité, ça donne 9 >= 33, à toi de voir si c'est vrai. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 15:38 Dim 08 Aoû 2010, 15:38 | |
| - oussama1305 a écrit:
Prends x = 3^{1/3}, qui est le cas d'égalité, ça donne 9 >= 33, à toi de voir si c'est vrai. Certes. Mais ce n'est pas de ma faute si mon moteur de calcul a déconné  | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 16:44 Dim 08 Aoû 2010, 16:44 | |
| - Abdek_M a écrit:
- elle equivaut à

ce qui est vrai par Am-Gm Bien vu Abdek !  Sinon voici la solution que j'ai trouvé à première vue : On pose :  L'inégalité est homogène, nous pouvons donc supposer que :  L'inégalité équivaut à :    Ce qui est clairement vrai.
Dernière édition par King le Ven 10 Sep 2010, 02:11, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 17:14 Dim 08 Aoû 2010, 17:14 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 17:32 Dim 08 Aoû 2010, 17:32 | |
| - oussama1305 a écrit:
Il m'a semblé voir :
- King a écrit:
- L'inégalité est homogène, nous pouvons donc supposer que :
 Pardon. Quelqu'un aurait-il la tendresse, dans ce cas, d'expliquer comment l'on passe de la forme classique (pour t=1) : x(x − y)(x − z) + y(y − x)(y − z) + z(z − x)(z − y) >= 0, à la forme qu'a utilisé King : r >= (4q-1)/9 ? | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 | |
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  Dim 08 Aoû 2010, 17:47 Dim 08 Aoû 2010, 17:47 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Facile, mais pas futile. Sujet: Re: Facile, mais pas futile.  | |
| |
|
  | |
| | Facile, mais pas futile. |  |
|
