Epreuve 4 d'olympiade maroccain, 1ér SM, 1987

Un sujet d'une difficulté moyenne, je vais présenter les solutions des trois exercices 1, 3, et 4.
Je commence par le troisième:
On a .==>(1)
Remplaçons x par 1-x, alors .
Donc .
Donc .==>(2)
En sommant 1 et 2, on trouve que .
Donc .
Donc .
Et puisque a+b est différent de 0, il vient que .
Donc .
En remplaçant dans 1, il s'ensuit que .
Donc .
Donc .
Et puisque a-b est différent de 0, il vient que .
Réciproquement, soit f la fonction définie par .
On a .
Et on a .
Donc .
Donc .
En sommant, on trouve .
Donc .
Donc .
Donc .
Ainsi la seule fonction qui satisfait notre énoncé est la fonction .
Sauf erreur.

Pour le premier exercice, exercice de collège:
On veut démontrer que .
Procédons par équivalence:
On a .
Donc .
Donc .
Et puisque tout est positif, il vient que .
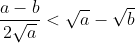Donc .
Donc .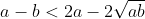
Donc .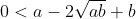
Donc .
Ce qui est juste.
De même pour l'autre côté.
On déduit directement que .
Sauf erreur.

Pour le troisième:
Après dessiner une figure, voici la solution que j'aime que quelqu'un se sent libre d'avoir le soin de la vérifier.
Soit O le centre du cercle (C) donné initialement, son rayon est r.
Soit (C') le cercle de centre B et de rayon AB.
Soit F le point d'intersection de (BD) et de (C).
On a BDC un triangle équilatéral.
Donc BDC=60°, DCB=60°, et CBD=60°. (angles)
Dans le cercle (C'), on a DAC un angle inscrit et DBC un angle au centre, deux angles limitant le même arc.
Donc DAC=1/2*DBC. (angles)
Donc DAC=1/2*60°. (angle)
Donc DAC=30°. (angle)
Dans le cercle (C), on a DAC et EFC deux anghles inscrits limitant le même arc [EC].
Donc EFC=DAC. (angles)
Donc EFC=30°. (angle)
Et on a EOC un angle au centre et EFC un angle inscrit, deux angles limitant le même arc.
Donc EOC=2*EFC. (angles)
Donc EOC=2*30°. (angle)
Donc EOC=60°. (angle)
On a OC et OE sont deux rayons dans le cercle (C).
Donc EO=OC.
Donc le triangle EOC est isocèle en O.
Donc OEC=OCE. (angles)
Et on sait que la somme des mesures des angles d'un triangle vaut 180°.==>(*)
En utilisant *, dans le triangle EOC:
Donc EOC+OEC+OCE=180°. (angles)
Donc 60°+OEC+OCE=180°. (angles)
Donc 2OEC=120°. (angle)
Donc OEC=60°. (angle)
Et on a BCEF un quadrilatère inscriptible.
Donc FBC+FEC=180°. (angles)
Donc 60°+FEC=180°. (angles)
Donc FEO+OEC=120°. (angles)
Donc FEO+60°=120°. (angle)
Donc FEO=60°. (angle)
Soit M le point d'intersection des deux droites (OE) et (FC).
En utilisant *, dans le triangle EFM:
On a EFM+FEM+FME=180°. (angles)
Donc 30°+60°+FME=180°. (angle)
Donc FME+90°=90°. (angle)
Donc FME=90°. (angle)
En utilisant *, dans le triangle OMC:
On a OMC+MOC+MCO=180°. (angles)
Donc 90°+60°+MCO=180°. (angle)
Donc 150°+MCO=180°. (angle)
Don MCO=30°. (angle)==>(1)
D'autre part, on a BO=OC car (BO) et (OC) sont deux rayons dans le même cercle.
Et on a DC=DB car le triangle BDC est équilatéral.
Donc (DO) est médiatrice du segment [BC].
Soit N l'intersection de (DO) et (BC).
En utilisant *, dans le triangle DNB:
On a BDN+DNB+NBD=180°. (angles)
Donc BDN+90°+60°=180°. (angle)
Donc BDN+150°=180°. (angle)
Donc 180°-NDF+150°=180°. (angle)
Donc NDF=150°. (angle)==>(2)
Dans le quadrilatère DOCF, et selon 1 et 2, on a FDO+OCF=180°.
Donc le quadrilatère DOCF est inscriptible.==>(3)
On a OCE=60°. (angle)
Donc OCM+MCE=60°. (angles)
Donc 30°+MCE=60°. (angle)
Donc MCE=30°. (angle)
Et puisque MFE=30°, il vient que le triangle FEC est isocèle en E.
Donc EF=EC.
Et on a EO=EC, selon ce qui précède.
Donc EO=EC=EF=r.
Et selon 3, on déduit que ED=r.
CQFD.