Sommes avec arctan.

je vous propose de calculer ces deux sommes :


Bonne chance

tarask a écrit:

je vous propose de calculer ces deux sommes :


Bonne chance

On utilise la propriété suivante, facilement démontrable :

Pour a=k+2 et b=k, on trouve :

Et on procède par téléscopage.
Même chose pour S', en posant : .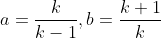
À la fin, un petit calcul donne, si je ne me trompe :

عيد مبارك سعيد و كل عام و أنتم بخير

Bonjour
pour la première somme elle est parfaite
la deuxième j'ai un petit doute en posant 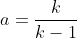,pour procéder par télescopage on aura un problème avec k=1 nn?
sauf erreur
EDIT: ça y est je crois que vous avez fait S'n=arctan(1/2) + sigma (de k=2 à n) de ce qui reste ! je viens de le voir .....

Merci pour ton intérêt

pour la 2 eme :

En remarque que : arctg (k/k+1) -artg (k-1/k) = artg (1/k^2)

donc : sigma ( k = 1 --> n ) artg ( 1/ k^2 ) = ( k = 1 --> n ) [ artg (k/k+1 ) - artg (k-1 /k) ]

puis on utilise la somme telescopique :

alors : sigma ( k = 1 --> n ) artg ( 1/ k^2 ) = artg ( n/n+1) - artg (0)

donc : sigma ( k = 1 --> n ) artg ( 1/ k^2 ) = artg (n/n+1)

SQFD

sauf erreur B1 sur