reeos
Débutant
 Nombre de messages : 3
Age : 30
Date d'inscription : 15/09/2010
 | | Sujet: exo math Mer 15 Sep 2010, 16:09 | |
| bonjour!!
voilà cet exo me tourmente depuis bien qqs jours !!
^prenons x et y ,deux nombres réels tel que !x! =< 1/2 et !y!=<1
demontrer que !4x²y - y - x!=< 17/16
(en utilisant "al istilsame")
D avance ,j estimerai votre aide tres précieux à mon égard
NB : !x! =x القيمة المطلقة ل | |
|
nmo
Expert sup
 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: exo math Mer 15 Sep 2010, 16:39 | |
| Tu peux, soit voir ici: https://mathsmaroc.jeun.fr/inegalites-f2/inegalite-tc-t16258.htm. Soit t'efforcer en cherchant personellement ta propre solution. Tu n'as qu'à te reférer de la solution guidée de l'exercice 67, qui se trouve à la page 366. Au pire des cas, si tu ne parviens à rien. Je vais enrichir la solution du livre. Au plaisir. | |
|
reeos
Débutant
Nombre de messages : 3
Age : 30
Date d'inscription : 15/09/2010
| | Sujet: Re: exo math Lun 20 Sep 2010, 21:06 | |
| oui oui s il vous plait ca serait vraiment tres gentil de votre part si vous m y trouvez la solution!!  | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: exo math Mar 21 Sep 2010, 17:15 | |
| Comme tu veux mon cher, On pose =4x^2y-y-x) . Donc =y(4x^2-1)-x) . Ainsi f est une fonction affine. D'autre part, on a 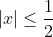 . Donc 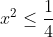 . Donc 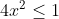 . Donc 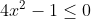 . Donc le coéficient de y dans la fonction affine est négatif. Ce qui veut bien dire que la fonction f est décroissante sur l'intervalle [-1,1]. On a 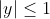 . Donc 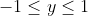 . Donc \le f(y)\le f(-1)) .==>(1) D'un autre côté, on a =-1*(4x^2-1)-x) . Donc =-(4x^2-1+x)) . Donc =-\big((2x)^2+2*2x*\frac{1}{4}+\frac{1}{16}-\frac{1}{16}-1\big)) . Donc =-\big((2x+\frac{1}{4})^2-\frac{17}{16}\big)) . Donc =-(2x+\frac{1}{4})^2+\frac{17}{16}) . Donc ^2=\frac{17}{16}-f(-1)) . Or, on a pour tout réél x, ^2\ge0) . Donc \ge0) . Donc ) .==>(2) De la même manière, on aboutit à \ge-\frac{17}{16}) .==>(3) De 1 et 2 et 3, on trouve que \le f(y)\le f(-1)\le\frac{17}{16}) . Soit \le\frac{17}{16}) . Donc |\le\frac{17}{16}) . Donc 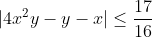 . CQFD. L'égalité aura lieu si \in\{(-1,-\frac{1}{8}),(1,\frac{1}{8})\}) . Sauf erreur.
Dernière édition par nmo le Ven 24 Sep 2010, 10:38, édité 1 fois (Raison : Erreur de signes) | |
|
W.Elluizi
Maître
Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
| | Sujet: Re: exo math Mar 21 Sep 2010, 17:31 | |
| Du bon boulot Nmo,J'étais justement sur le point de rédiger une solution identique à la tienne,mais maintenant ,ce n'est plus la peine.Encore une fois bravo nmo! | |
|
chamitos007
Maître
Nombre de messages : 163
Age : 30
Date d'inscription : 27/12/2009
| | Sujet: Re: exo math Mer 22 Sep 2010, 21:55 | |
| bein c'est facile tu peux voir la solution dans un solutionnaire comme dima dima ou top cet exercice se répète partout et merci nmo pour cette belle méthode car on veut changer un petit peu hh  | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: exo math Dim 26 Sep 2010, 16:41 | |
| - chamitos007 a écrit:
- bein c'est facile tu peux voir la solution dans un solutionnaire comme dima dima ou top cet exercice se répète partout et merci nmo pour cette belle méthode car on veut changer un petit peu hh
Oui, en effet, le solutionnaire TOP présente une autre methode. Personnelement, je ne dispose que de DIMA DIMA, et j'ai vu l'exercice quand un camarade m'a laissé voir ce TOP. Il serait gentil de ta part d'écrire cette methode. | |
|
reeos
Débutant
Nombre de messages : 3
Age : 30
Date d'inscription : 15/09/2010
| | Sujet: Re: exo math Jeu 07 Oct 2010, 21:43 | |
| | |
|
