| | ensembles |  |
|
|
| Auteur | Message |
|---|
princessdesmaths
Maître

 Nombre de messages : 149 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 |  Sujet: ensembles Sujet: ensembles  Jeu 14 Oct 2010, 19:17 Jeu 14 Oct 2010, 19:17 | |
| soit E ensemble , A et B des parties de E : trouvez une condition suffisante pour que l'equation ait au moin une solution :(A n X) =B  | |
|
  | |
afoukal.maths
Féru
 Nombre de messages : 33 Nombre de messages : 33
Age : 30
Localisation : centre de pythagore pres de £
Date d'inscription : 01/03/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Jeu 14 Oct 2010, 19:34 Jeu 14 Oct 2010, 19:34 | |
| | |
|
  | |
princessdesmaths
Maître

 Nombre de messages : 149 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Jeu 14 Oct 2010, 19:46 Jeu 14 Oct 2010, 19:46 | |
| je crois pas que c'est la bonne reponse , j'ai trouvé autre chose !!! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Jeu 14 Oct 2010, 20:09 Jeu 14 Oct 2010, 20:09 | |
| B C A est une condition suffisante.
En effet, sous cette condition, X=B est une solution. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Jeu 14 Oct 2010, 20:23 Jeu 14 Oct 2010, 20:23 | |
|
salam
n : inter
c : inclus
__________
A n X = B
B n A n X = B n B = B
===> B c AnB
or AnB c B
===> AnB = B ===> B c A ( condition nécessaire)
et c'est aussi suffisante.
.
| |
|
  | |
princessdesmaths
Maître

 Nombre de messages : 149 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Jeu 14 Oct 2010, 21:28 Jeu 14 Oct 2010, 21:28 | |
| oui c'est ça la condition necessaire est BcA  !!! | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Dim 17 Oct 2010, 11:13 Dim 17 Oct 2010, 11:13 | |
| svp de l'aide!!!!
trouver les solutions de l'équation
A ⋂ X = B
J'ai trouvé une solution dans DIMA DIMA mais je l'ai vraiment pas comprise! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Dim 17 Oct 2010, 12:26 Dim 17 Oct 2010, 12:26 | |
| Supposons que A ⋂ X = B et soit x un élément de X. x appartient à A <=> x appartient à B. Donc : [(x appartient à A) et (x appartient à B)] ou [(x n'appartient pas à A) et (x n'appartient pas à B)] Donc : %20\cup%20(\overline{A}%20\cap%20\overline{B})) Donc : %20\cup%20(\overline{A}%20\cap%20\overline{B})) Et puisque BCA est une condition nécessaire pour que l'équation ait un sens, alors : 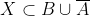 De plus, 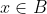 => 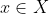 . Donc 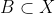 Inversement, supposons que 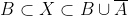 et montrons que A ⋂ X = B. Soit 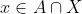 . => 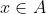 et 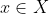 => 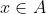 et 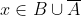 => )) => ) => 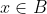 Donc 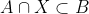 . Soit 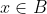 . => 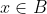 et 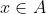 => 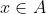 et 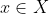 => ) Donc 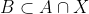 . Par conséquent, 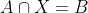 . Synthèse :Les ensembles solutions sont les ensembles X tels que 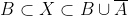 .
Dernière édition par Dijkschneier le Dim 17 Oct 2010, 12:49, édité 2 fois | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Dim 17 Oct 2010, 12:46 Dim 17 Oct 2010, 12:46 | |
| et c'est quoi la solution de l'équation dans ce cas? | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Dim 17 Oct 2010, 12:55 Dim 17 Oct 2010, 12:55 | |
| Merciii beaucoup juste une autre petite question
Pourquoi on a ajouté l'étape d'inversement?
Bon ce que j'ai compris c'est que quand on nous demande de résoudre une équation comme celle-ci il faut trouver où se trouve le X et pour celle-là on suppose que x appartient à X et on commence a déduire c'est ça ou bien j'ai rien compris? :p | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Dim 17 Oct 2010, 13:03 Dim 17 Oct 2010, 13:03 | |
| - soumitous a écrit:
- Merciii beaucoup juste une autre petite question
Merci. Des personnes qui remercient ceux qui leur ont apporté une aide, ça se fait de plus en plus rare sur ce forum ! - soumitous a écrit:
Pourquoi on a ajouté l'étape d'inversement?
Bon ce que j'ai compris c'est que quand on nous demande de résoudre une équation comme celle-ci il faut trouver où se trouve le X et pour celle-là on suppose que x appartient à X et on commence a déduire c'est ça ou bien j'ai rien compris? :p Il faut en effet trouver où se trouve le X. On fait donc, comme tu l'as dit, un ensemble de déductions qui nous permettent de savoir où le X doit se trouver. Mais on ne sait pas encore s'il existe un X parmi cet ensemble réduit d'hypothétiques solutions vérifiant en effet l'équation. Il nous faut donc procéder à une seconde étape : montrer que tous les ensembles appartenant à cet ensemble réduit d'hypothétiques solutions soient tous des solutions effectives à l'équation. C'est l'intéret de l'"inversement". Ce qu'on fait est donc exactement : - Si X vérifie l'équation, alors X doit se trouver dans un ensemble réduit S. - Si X appartient à l'ensemble S, alors il vérifie l'équation. Donc S est l'ensemble des solutions de l'équation. | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: ensembles Sujet: Re: ensembles  Dim 17 Oct 2010, 13:25 Dim 17 Oct 2010, 13:25 | |
| J'ai vraiment compris maintenant merci mais beaucoup juste que j'ai quelque problème d'application xD
Donc maintenant pour A U X = B x appartient à X
Donc x appartient à B alors X C B
et là je dois faire l'inversement je dis:
X C B donc x appartient a X => x appartient à B c'est ça ou bien j'ai tout foiré xD | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: ensembles Sujet: Re: ensembles  | |
| |
|
  | |
| | ensembles |  |
|
