| | calcule d'une somme_oral X |  |
|
|
| Auteur | Message |
|---|
Fermat-X
Maître
 Nombre de messages : 99
Age : 31
Date d'inscription : 22/11/2008
| | Sujet: calcule d'une somme_oral X Ven 22 Oct 2010, 21:12 | |
| -Calculer 1*2*3+2*3*4+......+1000*1001*1002
-on demande en faite une méthode générale plus calculer S=[sigma de p=0 à n] (p+1) ....(p+k)
| |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: calcule d'une somme_oral X Sam 23 Oct 2010, 23:35 | |
| - Fermat-X a écrit:
- -Calculer 1*2*3+2*3*4+......+1000*1001*1002
-on demande en faite une méthode générale plus calculer S=[sigma de p=0 à n] (p+1) ....(p+k)
Je pense avoir déjà vu la généralisation du premier calcul. Si je me rappelle bien, c'est : (k+2)=\frac{n(n+1)(n+2)(n+3)}{4}) Assurons-nous de cela en usant d'un raisonnement par récurrence : Nous avons : (1+2)(1+3)}{4}) Donc la proposition est vraie pour 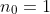 Supposons qu'elle est vraie pour n et démontrons-la pour n+1 : (k+2)=(n+1)(n+2)(n+3)+\sum_{k=1}^{n%20}k(k+1)(k+2)=(n+1)(n+2)(n+3)+\frac{(n+1)(n+2)(n+3)(n+4)}{4}=(n+1)(n+2)(n+3)\left%20(%20\frac{n}{4}+1%20\right%20)=\frac{(n+1)(n+2)(n+3)(n+4)}{4}) Donc pour tout n de N*, la proposition est vraie. La suite est facile, je crois... Pour la deuxième question, j'y réfléchirai. Au plaisir ! | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: calcule d'une somme_oral X Dim 24 Oct 2010, 11:05 | |
| Pour la deuxième question, on peut considérer un polynôme P du (k+1)ème degré tel que pour tout réel x, P(x+1)-P(x)=x(x+1)(x+2)...(x+k).
Il s'agit donc d'écrire explicitement P, en résolvant l'équation polynomiale indiquée plus haut.
P(n) sera alors le résultat escompté. | |
|
| | |
Fermat-X
Maître
Nombre de messages : 99
Age : 31
Date d'inscription : 22/11/2008
| | Sujet: Re: calcule d'une somme_oral X Dim 24 Oct 2010, 17:15 | |
| | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: calcule d'une somme_oral X Mar 09 Nov 2010, 22:31 | |
| - Dijkschneier a écrit:
- Pour la deuxième question, on peut considérer un polynôme P du (k+1)ème degré tel que pour tout réel x, P(x+1)-P(x)=x(x+1)(x+2)...(x+k).
Il s'agit donc d'écrire explicitement P, en résolvant l'équation polynomiale indiquée plus haut.
P(n) sera alors le résultat escompté. Oui, mais l'équation polynomiale est-elle facile à résoudre ?... | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: calcule d'une somme_oral X Mer 10 Nov 2010, 13:44 | |
| - mizmaz a écrit:
- Dijkschneier a écrit:
- Pour la deuxième question, on peut considérer un polynôme P du (k+1)ème degré tel que pour tout réel x, P(x+1)-P(x)=x(x+1)(x+2)...(x+k).
Il s'agit donc d'écrire explicitement P, en résolvant l'équation polynomiale indiquée plus haut.
P(n) sera alors le résultat escompté. Oui, mais l'équation polynomiale est-elle facile à résoudre ?... Bien sûr : identification directe des coefficients de chaque membre. | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: calcule d'une somme_oral X Mer 10 Nov 2010, 21:09 | |
| Hum... Peux-tu le faire dans ce cas ? Sinon, il est facile de démontrer l'égalité suivante par récurrence : +...+n(n+1)(n+2)...(n+k-1)=\frac{n(n+1)(n+2)...(n+k)}{k+1}) | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: calcule d'une somme_oral X Mer 10 Nov 2010, 23:04 | |
| - mizmaz a écrit:
- Hum... Peux-tu le faire dans ce cas ?
Sinon, il est facile de démontrer l'égalité suivante par récurrence :
Les développements sont houleux mais je crois toujours qu'on peut y arriver à bout. Usage intensif de la formule du binôme. Par contre, il est vrai que la formule que tu viens de proposer est bien plus agréable à manipuler. | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: calcule d'une somme_oral X Jeu 11 Nov 2010, 19:56 | |
| La formule est également une solution à l'équation polynomiale ! (Il suffit en effet de remplacer les n par des x.  ) Au plaisir ! | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: calcule d'une somme_oral X Jeu 11 Nov 2010, 20:01 | |
| - mizmaz a écrit:
- La formule est également une solution à l'équation polynomiale ! (Il suffit en effet de remplacer les n par des x. )
Au plaisir ! Oui, et par unicité de la solution (l'étape d'identification des coefficients impose l'unicité), elle est la seule. | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: calcule d'une somme_oral X | |
| |
|
| | |
| | calcule d'une somme_oral X | |
|
