Un Oral !!

Posons
,
avec est la somme de diviseur de , soit un entier naturel strictement postif ,Montrer que l'equation

possède une infinité de solutions .

Soit m un entier >0( suffisamment grand) et p le plus grand nombre premiers inférieur à :

Alors les nombres de l'ensemble sont tous composés .
Pour simplifier on pose ( s=m!+m-p )
Soit (p+k) un entier de E . k£{1,2,...r} et a un entier de{1,2,..k} .
Avec r un entier qui vérifie
Puisque (p+a) est composé alors :


Donc on a :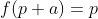

et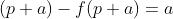

En répétant le même processus avec des entier M >m on obtient une infinité de solution pour l'équation :
p-f(p)=k ..
Sauf erreur

Bravo Baraa !! c'est ça l'idée