une limite !

déterminer

Discipliné a écrit:

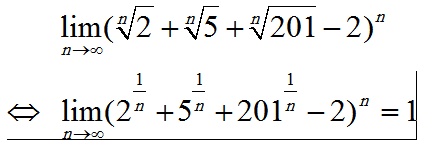Non, ce n'est pas aussi simple que ça.

mizmaz a écrit:

Discipliné a écrit:

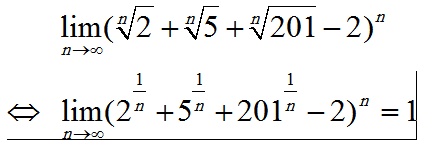Non, ce n'est pas aussi simple que ça.

C'est ce que j'ai pensé ...
Qu'est ce que tu penses?

la limite = 2010 mais j'ai pas encore trouvé la methode

si ce n'est pas 1 ou est la faute de discipline ainsi? svp!!
amicalement

lim(1^x) x-> infinie c'est une forme indeterminé

nadia93 a écrit:

lim(1^x) x-> infinie c'est une forme indeterminé

t'es sûre ? je crois que c plutôt lim (x->+infini) f(x)^x qui est une forme indéterminé si lim (x->+infini) f(x)=1.

(V x £ IR) 1^x=1 non ?

oui t'as raison dsl
mais je suis sure que cette limite =/= 1 mais 2010 je l'ai calculé avec un logiciel mais j'ai pas encore trouver la methode
lore je croix la faute c'etait le faite d'ecrire rac n eme en 1/n

pourquoi ce faite de l'ecrire est une faute ? je ne vois pas la raison. et plutot pour prouver
que lim(x->+oo)[1^x]=1 sufit de decouper 1^x=1*1*1*1*1*...........
ainsi lim(x->+oo)[1^x]=lim(x->+oo)[1]*lim(x->+oo)[1]*lim(x->+oo)[1]*......
=1*1*1*1*1......................
=1
sauf erreur.
amicalement

nn nn la faute c juste d'avoir considéré lim (n->+infini,f(n)^n)=1 puisque
lim (n->+infini,f(n))=1 parce qu'au fait lim (n->+infini, f(n)^n)=lim(n->+infini,e^(nln(f(n)))) ce qui donne la forme indéterminée 0*+infini

ah j'ai commpri mnt merci
^^

Je crois avoir trouvé la solution (sauf erreur) c'est effectivement 2010 ^^

Je la posterai dans quelques minutes

la Voilà désolé si ce n'est pas lisible

https://2img.net/r/ihimg/photo/my-images/808/numriser0002z.jpg/

SherlocK a écrit:

la Voilà désolé si ce n'est pas lisible

https://2img.net/r/ihimg/photo/my-images/808/numriser0002z.jpg/

Pour faire une conclusion.
C'est quoi la faute qu'il faut éviter et à quoi faire attention dans ce genre de limite?
Et Comment savoir si c'était une forme indéterminée où pas si on trouve une limite fini?
Merci.

Discipliné a écrit:

SherlocK a écrit:

la Voilà désolé si ce n'est pas lisible

https://2img.net/r/ihimg/photo/my-images/808/numriser0002z.jpg/

Pour faire une conclusion.
C'est quoi la faute qu'il faut éviter et à quoi faire attention dans ce genre de limite?
Et Comment savoir si c'était une forme indéterminée où pas si on trouve une limite fini?
Merci.

Je crois que ça répond à tes questions ^^ :

Citation :

la faute c juste d'avoir considéré lim (n->+infini,f(n)^n)=1 puisque
lim (n->+infini,f(n))=1 parce qu'au fait lim (n->+infini, f(n)^n)=lim(n->+infini,e^(nln(f(n)))) ce qui donne la forme indéterminée 0*+infini

Ta réponse aurait été juste si (V n £ IN) f(n)=1 mais elle tend vers 1 quand n tend vers +infini ce qui a provoqué la forme indéterminée.

SherlocK a écrit:

la Voilà désolé si ce n'est pas lisible

https://2img.net/r/ihimg/photo/my-images/808/numriser0002z.jpg/

Perfect