| | Olympiade TSM n°6 |  |
|
+5nmo isma.lem louis mizmaz Dijkschneier 9 participants |
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Olympiade TSM n°6 Sujet: Olympiade TSM n°6  Ven 06 Mai 2011, 18:12 Ven 06 Mai 2011, 18:12 | |
| Exercice 1 :
Trouver tous les entiers x,y et z vérifiant : x+y+z=4022 et x²+y²+z²=2(yz+1)
Exercice 2 :
Soient a,b et c trois nombres réels strictement positifs.
Montrer que : sqrt(a²+b²+sqrt(2)ab) + sqrt(b²+c²-sqrt(2)bc) >= sqrt(a²+c²)
Exercice 3 :
Un tournoi de tennis a eu au moins trois participants. Lors du tournoi, chaque deux joueurs ont joué exactement une fois l'un contre l'autre et chaque joueur a gagné au moins un match.
Montrer qu'il existe trois joueurs A, B et C tels que A a battu B, B a battu C et C a battu A.
Exercice 4 :
Cinq points A,B,C,D et E sont, dans cet ordre, sur un cercle de rayon r tels que AC=BD=CE=r.
Soient P, Q et R les orthocentres des triangles ACD, BCD et BDE.
Montrer que le triangle PQR est rectangle. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 18:33 Ven 06 Mai 2011, 18:33 | |
| J'ai trouvé une solution très élégante je trouve au problème 2 :
Il suffit de prendre un triangle ABC rectangle en B tel que AB=a et BC=c puis de prendre un point D de la bissectrice de l'angle ABC tel que BD=b. Et le problème devient équivalent à CD+AD >= AC. Ce qui est vrai par l'inégalité triangulaire. Sauf erreur.
Au plaisir !
Dernière édition par mizmaz le Sam 07 Mai 2011, 13:43, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 18:46 Ven 06 Mai 2011, 18:46 | |
| Oh ! Joli... Par contre, pour le problème 4 :  WTF ??! | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 18:47 Ven 06 Mai 2011, 18:47 | |
| Pour l'exercice 1: =2yz+2\Leftrightarrow x^2+(y-z)^2=2) ^2=2\Leftrightarrow x=1 \text{et} y-z=1) D'autre part on substitue la valeur de x dans la première égalité, on trouve 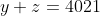 Après des simples calculs on trouve dans 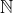 \}) Dans 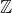 on trouve \}) D'ou ;(-1,2011,2012)\})
Dernière édition par louis le Ven 06 Mai 2011, 20:02, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 18:51 Ven 06 Mai 2011, 18:51 | |
| | |
|
  | |
isma.lem
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 48
Date d'inscription : 02/03/2011
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 19:00 Ven 06 Mai 2011, 19:00 | |
|
Exercice 2 :
Soient a,b et c trois nombres réels strictement positifs.
Montrer que : sqrt(a²+b²+sqrt(2)ab) + sqrt(b²+c²-sqrt(2)bc) >= sqrt(a²+c²)
[/quote]
Ca ne serait pas sqrt(a²+b²6sqrt(2)ab) plutôt ?
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 19:20 Ven 06 Mai 2011, 19:20 | |
| Je fais ma solution pour le deuxième problème: Soient x, y, z, et t des réels positifs. Selon l'inégalité de Caushy-schwartz, on a: (z^2+t^2)}\ge xz+yt&\Leftrightarrow2\sqrt{(x^2+y^2)(z^2+t^2)}\ge 2xz+2yt\\&\Leftrightarrow x^2+y^2+2\sqrt{(x^2+y^2)(z^2+t^2)}+z^2+t^2\ge x^2+2xz+z^2+y^2+2yt+t^2\\&\Leftrightarrow\big(\sqrt{x^2+y^2}+\sqrt{z^2+t^2}\big)^2\ge (x+z)^2+(y+t)^2\\&\Leftrightarrow\sqrt{x^2+y^2}+\sqrt{z^2+t^2}\ge\sqrt{(x+z)^2+(y+t)^2}\end{align*}) . On prends:  ,  , et  , on trouve: ^2+(\frac{\sqrt{2}}{2}.b)^2}+\sqrt{(c-\frac{\sqrt{2}}{2}.b)^2+(\frac{\sqrt{2}}{2}.b)^2}\ge\sqrt{(a-\frac{\sqrt{2}}{2}.b+\frac{\sqrt{2}}{2}.b)^2+(c-\frac{\sqrt{2}}{2}.b+\frac{\sqrt{2}}{2}.b)^2}&\Leftrightarrow\sqrt{a^2-2.\frac{\sqrt{2}}{2}.ab+2(\frac{\sqrt{2}}{2}.b)^2}+\sqrt{c^2-2.\frac{\sqrt{2}}{2}.bc+2(\frac{\sqrt{2}}{2}.b)^2}\ge\sqrt{(a)^2+(c)^2}\\&\Leftrightarrow\sqrt{a^2-\sqrt{2}.ab+2.\frac{1}{2}b^2}+\sqrt{c^2-\sqrt{2}.bc+2.\frac{1}{2}b^2}\ge\sqrt{(a)^2+(c)^2}\\&\Leftrightarrow\sqrt{a^2+b^2-\sqrt{2}.ab}+\sqrt{c^2+b^2-\sqrt{2}.bc}\ge\sqrt{(a)^2+(c)^2}\end{align*}) . Cette démonstration est valable si et seulemùent si  et  . Elle est valable dans tous les autres qui restent, car: :\alpha^2=(-\alpha)^2) . Ainsi: ^2+(c)^2}) . CQFD. Sauf erreur. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 19:23 Ven 06 Mai 2011, 19:23 | |
| Le quatrième est décidément faux. Je vais donc me suffire à poster une solution au troisième, qui, bien qu'assez facile dans l'ensemble, mérite tout de même une petite solution. Soit n le nombre des participants (joueurs) dans le tournoi de tennis. On considère un graphe orienté de n sommets s1, s2, s3, ..., sn, où chaque sommet représente un joueur différent. On relie deux sommets s(i) et s(j) par une arête orientée (une flèche) dirigée vers s(j) lorsque s(i) a vaincu s(j). On dira que s(i) et s(j) sont connectés s'il existe une flèche dirigée de s(i) vers s(j). On sait d'après les données que ce graphe est connexe (dans le sens où entre deux sommets quelconques il y a toujours une flèche). On suppose également sans perte de généralité que la configuration de départ est : s1 ---> s2 ---> s3 ---> ... ---> sn L'objectif est de montrer qu'il existe au moins un cycle de longueur 3. Supposons par l'absurde qu'il n'y ait aucun cycle de longueur 3, et montrons alors par une récurrence décroissante sur m que : (\forall%20i%20\in%20\mathbb{N^*}%20/%20m+i%20\in%20\{1,2,3,...,n\})%20:%20s_m%20\text%20{%20et%20}%20s_{m+i}%20\text%20{%20sont%20connect%C3%A9s}) - Pour m=n-1, c'est vrai puisque les seuls i tels que ((n-1)+i) appartient à {1,2,3,...,n} sont i=1, et s(n-1) et s(n) sont bien connectés d'après la configuration initiale. - Supposons que la propriété est vraie au rang m et montrons qu'elle l'est aussi au rang m-1. On choisit donc un i' tel que ((m-1)+i') soit dans {1,2,3,...,n}. Supposons que c'est s((m-1)+i') et s(m-1) (dans cet ordre) qui sont connectés. On applique l'hypothèse de récurrence au rang m avec i=i'-1 pour obtenir que s(m) et s((m-1)+i') sont connectés. Or s(m-1) et s(m) sont connectés d'après la configuration initiale. Et d'après notre supposition, s((m-1)+i') et s(m-1) sont connectés. On a donc le cycle de longueur 3 suivant : s(m) ---> s((m-1)+i') ---> s(m-1) ---> s(m), ce qui est une contradiction, et permet de conclure que c'est s(m-1) et s((m-1)+i') (dans cet ordre) qui sont connectés, et d'achever la récurrence et la preuve.
Dernière édition par Dijkschneier le Ven 06 Mai 2011, 19:29, édité 1 fois | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 19:29 Ven 06 Mai 2011, 19:29 | |
| - Dijkschneier a écrit:
Exercice 2 :
Soient a,b et c trois nombres réels strictement positifs.
Montrer que : sqrt(a²+b²-sqrt(2)ab) + sqrt(b²+c²-sqrt(2)bc) >= sqrt(a²+c²)
remplaçons a;bsqrt(2);c par x;y;z l'inégalité devient équivalent apres lever le tout au carré à :  ce qui est vrai par CS car :  | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 19:32 Ven 06 Mai 2011, 19:32 | |
| Problème 1.x²+y²+z²=2(yz+1) => |x|=|y-z|=1 Problème 2.poser (a/b) = xrac(2) et (a/c) = yrac(2), l'inégo equivaut après avoir simplifier et lever au carré à: [x²+(x-1)²][y²+(1-y)²]>= (x+y-1)² ce qui n'est rien que C-S. Problème 3.Soit P_1, P_2,...,P_n les participants,on note |P_n|, le nombre de victoires de P_n. Supposons que pour tous k et j, (P_k est victime de P_j => tous les victimes de P_k sont aussi victimes de P_j), dans ce cas supposons que P_1 a battu P_t alors il a battu tous les victimes de P_t et par conséquent |P_1|> |P_t| ce qui est absurde, d'où il existe j et k et r tel que P_r est victime de P_k, P_k est victime de P_j et P_j est victime de P_r. C.Q.F.D Problème 4.Il y a une faute dans ce problème comme Dijkschneier l'avait signalé, Le point R doit être l'orthocentre du triangle BCE. Pour laisser la chance aux autres pour le refaire, je présente ici une solution sans mots. 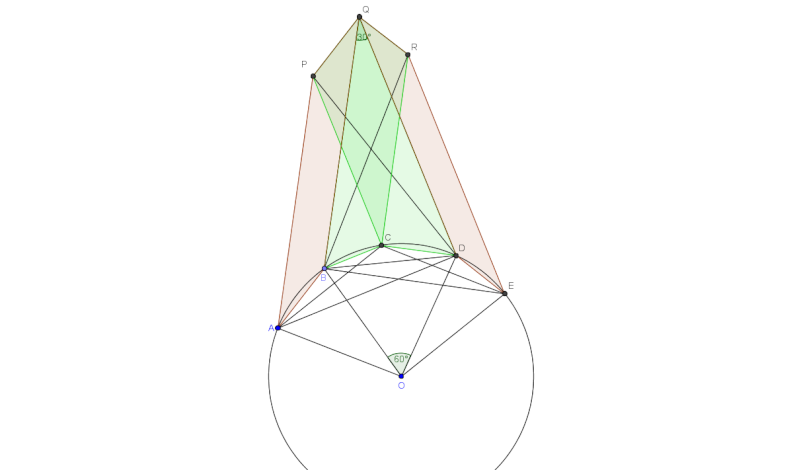 Commentaire. Commentaire. Deux Problèmes stupides (1 et 3) et une faute dans le quatrième problème, ce n'est pas ce dont on avait besoin. Je crois que vous partagez aussi mon opinion. | |
|
  | |
isma.lem
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 48
Date d'inscription : 02/03/2011
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 20:00 Ven 06 Mai 2011, 20:00 | |
| BTW, est-il vrai que même des élèves du sup peuvent se présenter pour les IMO ici au Maroc ? A ma connaissance c'est limité aux élèves de lycée. | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 20:03 Ven 06 Mai 2011, 20:03 | |
| - Dijkschneier a écrit:
- Entier ==> dans Z
Puisque tu n'as pas dit relatif ou naturel, j'ai fait l'étude sur IN. C'est édité. | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 21:27 Ven 06 Mai 2011, 21:27 | |
| - louis a écrit:
- Dijkschneier a écrit:
- Entier ==> dans Z
Puisque tu n'as pas dit relatif ou naturel, j'ai fait l'étude sur IN.
C'est édité. ça reste incomplet ! | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 21:39 Ven 06 Mai 2011, 21:39 | |
| - Sporovitch a écrit:
- louis a écrit:
- Dijkschneier a écrit:
- Entier ==> dans Z
Puisque tu n'as pas dit relatif ou naturel, j'ai fait l'étude sur IN.
C'est édité. ça reste incomplet ! Et maintenant ;(1,2010,2011);(-1,2011,2012);(-1,2012,2011)\}) ? | |
|
  | |
tahasinbad
Maître
 Nombre de messages : 158 Nombre de messages : 158
Age : 30
Date d'inscription : 02/12/2010
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 21:59 Ven 06 Mai 2011, 21:59 | |
| bonjour t le monde! pe etre je pense ke 12 eleves doivent partir : 6passent lepreuve et 6 autres remplacants! c vrai ?? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 22:25 Ven 06 Mai 2011, 22:25 | |
|
Dernière édition par Dijkschneier le Mar 05 Fév 2013, 04:31, édité 1 fois | |
|
  | |
tahasinbad
Maître
 Nombre de messages : 158 Nombre de messages : 158
Age : 30
Date d'inscription : 02/12/2010
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Ven 06 Mai 2011, 22:27 Ven 06 Mai 2011, 22:27 | |
| eh ben c ckoin ma di ss geurre sur! | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  Lun 29 Aoû 2011, 01:29 Lun 29 Aoû 2011, 01:29 | |
| Salut tout le monde, Je propose ma solution au problème 4 de géométrie : Solution au problème 4:Je commence tout d'abord par démontrer ce lemme qui est non-trivial : Lemme : Soit A,B,C,D quatres points cocyliques, vérifiant les conditions suivantes : AC=BD=R où R est le rayon du cercle circonscrit au quadrilatères ABCD, on note E et F les orthocentres respectifs des triangles BCD et ACD. Nous avons : AB=EF, et angle{FAB}=angle{FEB} 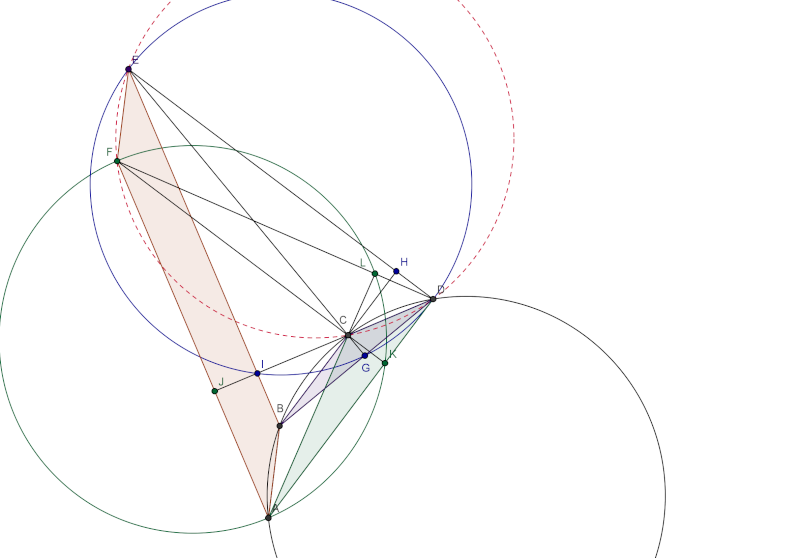 Preuve: Preuve: Tout d'abord, on note O le centre de (ABCD), H,G,I les projections orthogonales de D,C et B sur BC,BD et CD respectivement, de même on note L,K,J les projections orthogonales de D,C et A sur AC,AD et DC respectivement. Nous avons : angle{CDA}=1/2angle{COA}=1/2angle{BOD}=angle{BAD} et ainsi BC || AD, ce qui donne ABCD est un trapézoïde isocèle et ainsi AB=CD. D'autre part, nous avons FC est perpendiculaire à AD et ED est perpendiculaire à BC ce qui donne que les deux droites FC et ED sont parallèles. D'une autre part, nous avons les deux quadrilatères EDGI et FLKA sont inscriptibles et ainsi angle{DEC}=angle{DEG}=angle{DIG}=angle{CIG}, mais encore le quadrilatère CIBG est inscirptible et ainsi angle{CIG}=angle{CBG}=angle{CBD}=angle{CAD}=angle{LAK}=angle{LFK}=angle{DFC} et ainsi le quadrilatère EFCD est inscriptible et puisque ED || FC donc le quadrilatère EFCD est un trapézoïde isocèle et ainsi EF=CD=AB. D'autre part, il est bien clair que les deux droites AF et BE sont parallèles et ainsi : sin(FAB)=IJ/AB=IJ/EF=sin(FEB) et ainsi angle{FAB}=angle{FEB} vu qu'aucun des deux angles ne peut être obtus, sinon la démonstration restera similaire. Fin de la preuve du lemme.Revenons maintenat à notre problème : 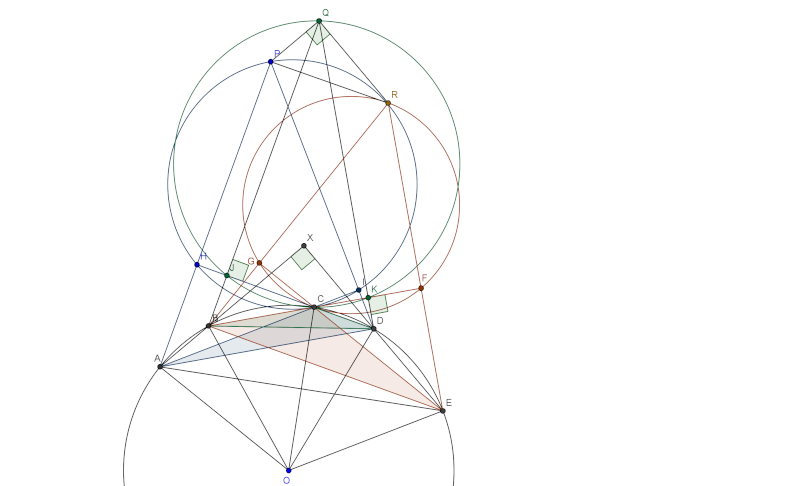 On introduit maintenant les points suivants ( qui sont différents de ceux du lemme), H et I les projetés orthogonales de A et D sur DC et AC, G et F les projetés orthogonales de B et E sur CE et BC, et J et K les projetés orthogonales de B et D sur CD et BC. Nous avons : angle{PAD}=angle{HAD}=90-angle{HDA}=90-angle{CDA}=90-1/2angle{AOC}=60. Ainsi angle{PAB}=angle{PAD}-angle{BAD}=60-30=30, de manière analogue on trouve : angle{DER}=30. Ainsi d'après le lemme en dessus on a : angle{RQD}=angle{PQB}=30. D'autre part puisque le quadrilatère JQKC est inscritpible donc : angle{BQD}=180-angle{BCD}=angle{BAD}=30 Finalement angle{PQR}=angle{RQD}+angle{BQD}+angle{PQB}=30+30+30=90. Et ainsi le triangle PQR est rectangle. P.S:Une solution bien plus courte existe en introduisant les nombres complexes, mais cela dit la méthode synthétique est beaucoup plus jolie. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiade TSM n°6 Sujet: Re: Olympiade TSM n°6  | |
| |
|
  | |
| | Olympiade TSM n°6 |  |
|
