Limites et continuité:

Démontrez à l'aide de la définition de la limite et de la continuité que:
1-La fonction sinus n'admet pas de limite en .
2-La fonction partie entière n'est pas continue en aucun point k appartenant à .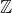
Bonne chance.

Pour la deuxième question:
f(x)= E(x) , Df= R
Soit k appartenant à Z, donc f(k)=E(k)=k

Limite à droite de K:

On a: quelque soit x de ]k,k+1[ : f(x)= E(x)= k

lim (x-->k+) f(x)= lim (x-->k+) E(x)= lim (x-->k+) k= k =f(k)

===> f est continue à droite de k.

Limite à gauche de K:

On considère le voisinage ]k-1,k[
On a: quelque soit x de ]k-1,k[ : E(x)= k-1

lim (x-->k-) f(x)= lim (x-->k-) E(x)= lim (x-->k-) k-1 = k-1 =/= f(k)

==> f n'est pas continue à gauche de k.

Synthèse:
f n'est pas continue en k / k de Z.

Sinon, pour la première on sait que sin(x) est périodique et -1=<sin(x) =<1 c'est pour cela qu'elle n'admet pas de limite en l'infini, on aura sûrement quelque chose par l'absurde...

Pour la premiere c'etait deja demontrer dans ce forum en utilisant les suites une fois, et par utilisation de definition aussi -par absurde bien sur- (tu peux le voir, c'est une methode de disjck[dont je ne suis pas convaincu])et la troisieme est ma facon propre que je vais la rediger plus tard..

Spoiler:

C'est juste kaj mima, mais je crois qu'il veut une solution en utilisant la définition epsilonesque...(c'est qu'une estimation suite a ce qu'il a ecri..)

Peux-tu poster le lien?
En attendant ta propre solution...

kaj mima a écrit:

Sinon, pour la première on sait que sin(x) est périodique et -1=<sin(x) =<1 c'est pour cela qu'elle n'admet pas de limite en l'infini, on aura sûrement quelque chose par l'absurde...

C'est effectivement ça ce qu'on doit démontrer: si f est une fonction périodique et bornée, alors elle n'admet pas de limite en .
Personnellement, cette propriété ne m'interesse pas pour le moment. Ce qui me préoccupe est la fonction sinus.
En effet, j'ai lu trois preuves -que je vais partager plus tard- sans savoir si c'est juste ou non.
Pour ta deuxième réponse, ce n'est plus cela ce que je veux, je cherche une solution avec les epsilons.

considerons f(x)=sinx
prouver que f n'admet pas de limite en
supposons par l'absurde qu'elle admet une limite L(l£R) en c.à.d: lim(x tend +infini)sinx=L
considerons les suites de points x_n=npi et y_n=pi/2 +2npi
on a lim(n tend +infini)x_n=+infini et lim(n tend +infini)y_n=+infini
donc
lim(x tend +infini)sin(x_n)=L et lim(x tend +infini)sin(y_n)=L
ce qui veut dire L=0 et L=1 ce qui est absurde.

Spoiler:

Oui c bien, c la meme que la tienne .J'ai fait le meme choix des x sauf que moi j'ai utilise la definition et j'ai trouve au premier cas au choix de epsilon=1 --> 0<y<1 et au deuxieme avec le meme choix d'epsilon -1<y<0 ce qui donne contradiction. Generalement la methode que tu as fait est la méthode des suites et peut etre applique a n'importe quelle fonction periodique ....