Marathon de problème-Polynômes-

Sujet: Marathon de problème-Polynômes- Jeu 12 Jan 2012, 22:20

Salut!
Je lance ce nouveau marathon de problèmes qui s'articule sur les polynômes
Les règles :
- Chaque participant ayant donné une solution doit se charger de proposer un nouveau problème. Si quelqu'un qui répond à un problème n'a pas de nouveau problème à proposer, qu'il l'indique clairement, et d'autres participant s'en chargeront de poster un.
-Numéroter clairement les problèmes et les solutions.
-Pas d'indice!Le propriétaire du problème peut posté sa solution après 1 semaine!
P#1:
Trouver tous les triplets (x,y,z) tels que :
x+y-z=0
zx-xy+yz=27
xyz=54

Sujet: Re: Marathon de problème-Polynômes- Ven 13 Jan 2012, 18:52

diablo902 a écrit:: P#1:
Trouver tous les triplets (x,y,z) tels que :
x+y-z=0
zx-xy+yz=27
xyz=54

salut a tous

Solution P#1 :
$Marathon de problème-Polynômes- Gif$

Sujet: Re: Marathon de problème-Polynômes- Ven 13 Jan 2012, 19:41

P#2 :
Soit P un polynôme a coeﬃcients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a)=b, P(b)=c et P(c) = a. Montrer que a=b=c.

Sujet: Re: Marathon de problème-Polynômes- Ven 13 Jan 2012, 20:41

Une autre S#1:
Soit x,y,-z les racines d'un polynôme P(x). D'après viète: p(x)=x^3-27x+54<==>p(x)=(x-3)²(x+6)d'où x=y=3 et z=6

Sujet: Re: Marathon de problème-Polynômes- Sam 14 Jan 2012, 18:29

abdelkrim-amine a écrit:: P#2 :
Soit P un polynôme a coeﬃcients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a)=b, P(b)=c et P(c) = a. Montrer que a=b=c.

nmo a écrit:

Dijkschneier a écrit:: Problème 18 :
Soit P un polynôme à coefficients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a) = b, P(b) = c et P(c) = a. Montrer que a = b = c.

Soit P un polynôme tel que $Marathon de problème-Polynômes- Gif.latex?p(x)=k_{n}x^{n}+k_{n-1}x^{n-1}+k_{n-2}x^{n-2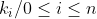}+..$ et avec $Marathon de problème-Polynômes- 0\le i\le n$ des entiers naturels.
On a P(a)=b, P(b)=c et P(c)=a.
Donc en sommant P(a)+P(b)à+P(c)=a+b+c.
Donc 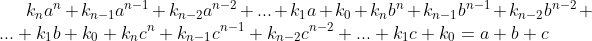$Marathon de problème-Polynômes- Gif.latex?k_{n}a^{n}+k_{n-1}a^{n-1}+k_{n-2}a^{n-2}+...+k_{1}a+k_{0}+k_{n}b^{n}+k_{n-1}b^{n-1}+k_{n-2}b^{n-2}+...+k_{1}b+k_{0}+k_{n}c^{n}+k_{n-1}c^{n-1}+k_{n-2}c^{n-2}+..$ .
Donc $Marathon de problème-Polynômes- Gif.latex?k_{n}(a^{n}+b^{n}+c^{n})+k_{n-1}(a^{n-1}+b^{n-1}+c^{n-1})+k_{n-2}(a^{n-2}+b^{n-2}+c^{n-2})+..$ .
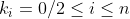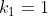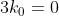Donc $Marathon de problème-Polynômes- 2\le i\le n$ , $Marathon de problème-Polynômes- Gif$ , et $Marathon de problème-Polynômes- Gif$ .
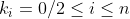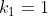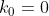Et ainsi $Marathon de problème-Polynômes- 2\le i\le n$ , $Marathon de problème-Polynômes- Gif$ , et $Marathon de problème-Polynômes- Gif$ .
Donc $Marathon de problème-Polynômes- Gif.latex?p(x)=0.x^{n}+0.x^{n-1}+0.x^{n-2}+...+1$ .
Donc $Marathon de problème-Polynômes- Gif$ .
D'où P(a)=a, P(b)=b et P(c)=c.
Donc a=b ,c=b , et a=c.
Par conséquent a=b=c.
CQFD.
Sauf erreur.

Dijkschneier a écrit:

nmo a écrit:: C'est quoi donc une égalité polynomiale.
En tout cas, je renonce.

Solution au problème 18 :
Ce problème est classique et est fondé sur le lemme suivant :
"Si P est un polynôme à coefficients entiers, alors pour tous entiers a et b, (a-b) divise (P(a)-P(b)). "
Revenons au problème.
Supposons par symétrie des rôles que a>=b>=c.
On a donc, d'une part : a-b divise P(a)-P(b), donc a-b divise b-c.
Et d'autre part, b-c divise P(b)-P(c), donc b-c divise c-a.
On en déduit que a-b divise c-a.
Or c-a divise a-b, car c-a divise P(c)-P(a), donc c-a divise a-b.
Par conséquent, |a-b|=|c-a|, et donc : a-b = a-c, b=c.
Et on prouve de même que |b-c|=|a-c|, et |a-b|=|b-c|.
On en déduit finalement que a=b=c.

Merci de le changer! Smile

Sujet: Re: Marathon de problème-Polynômes- Sam 14 Jan 2012, 22:46

P#3 :
Pour 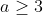$Marathon de problème-Polynômes- Gif$ , on considère le polynôme à coeﬃcients réels $Marathon de problème-Polynômes- Gif.download?P(x)=a_{n}x^n+..$
Prouver que P n’a pas toutes ses racines réelles.

» Marathon
» Marathon
» marathon mathématique
» Marathon
» Le marathon des énigmes.