inégalité triangulaire

Sujet: inégalité triangulaire Sam 28 Jan 2012, 14:30

prouver que si ABC un triangle:
9R²>=a²+b²+c² (R: le centre du cercle circonscrit)

Sujet: Re: inégalité triangulaire Dim 29 Jan 2012, 10:42

Salut,

Soit O le centre du cercle circonscrit à ABC, et soit R son rayon.
Soit H l'orthocentre du triangle ABC.

Par définition, on a : OH=OA+OB+OC

Donc OH.OH=OH²=OA²+OB²+OC²+2OA.OB+2OB.OC+2OA.OC

Or, (OB-OA)²=OB²+OA²-2OB.OA soit AB²=OB²+OA²-2OB.OA soit 2OB.OA=OB²+OA²-AB²

En permutant les lettres, on trouve : 2OB.OC=OB²+OC²-BC² et 2OA.OC=OA²+OC²-AC²

Au final, on obtient : OH²=3(OA²+OB²+OC²)-AB²-BC²-AC²=9R²-a²-b²-c²

Or, OH² >= 0 implique 9R² >= a²+b²+c²

Sauf erreurs.

Merci pour l'exo Smile

_________________

Ne rêve pas ta vie, vis tes rêves !

diablo902 a écrit:: prouver que si ABC un triangle:
9R²>=a²+b²+c² (R: le centre du cercle circonscrit)

Je propose une methode différente:
On pose 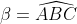$inégalité triangulaire Gif$ , $inégalité triangulaire Gif$ et $inégalité triangulaire Gif$ .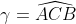
Et AB=c, BC=a et CA=b.
On a selon la loi des sinus: 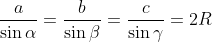$inégalité triangulaire Gif$ .
Donc 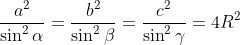$inégalité triangulaire Gif$ .
Et ainsi 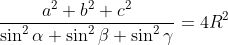$inégalité triangulaire Gif$ .
Ou bien $inégalité triangulaire Gif.latex?a^2+b^2+c^2=4R^2$ .
L'inégalité à démontrer devient 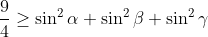$inégalité triangulaire Gif.latex?9R^2\ge4R^2$ .
Ou bien $inégalité triangulaire Gif$ .
Ce qui est vrai d'après l'inégalité de la convexité (de Jensen) (appliqué sur la fonction $inégalité triangulaire Gif$ sur l'intervalle [ 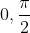$inégalité triangulaire Gif$ ].

» Inégalité triangulaire
» inegalite triangulaire
» les fonctions triangulaire
» inegalite triangulaire
» Utilisation de l'inégalité Triangulaire (ou pas )