- diablo902 a écrit:
- Soit
 un triangle tel que
un triangle tel que  et
et 
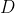 est le pied de la hauteur issue de
est le pied de la hauteur issue de  sur
sur  et
et  le pied de la hauteur issue de
le pied de la hauteur issue de 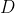 sur
sur 
Soit 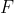 un point du segment
un point du segment 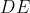 tel que :
tel que :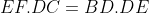
Démontrer que\perp&space;(BF)})
Je propose une réponse pour cet exercice:
Il est bien clair que les deux triangles AED et ADC sont semblables.
Ainsi, on aura la relation suivante:

.==>(1)
De plus, en calculant la surface du triangle ADC de deux manières différentes on trouve que
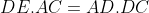
, ce qui implique que

.
Or, la condition de l'hypoyhèse implique que

.
En combinant ces deux dernières égalité, on tombe sur

.==>(2)
De 1 et 2, on trouve que

.
Et puisque les deux angles

et

sont égaux (car ils sont droits), il vient que les deux triangles AEF et ADB sont semblables.
Il s'ensuit que

.
Et puisque

, il vient

.
On en conclut que le quadrilatère ABDF est inscriptible.
Ainsi les deux angles

et
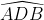
sont égaux, car ils intercèptent le même arc [AB] dans le cercle circonscrit au quadrilatère ABFD.
D'où le résultat.
Sauf erreur.
