Trouver K_{max}

Trouver la valeur max de k tel que pour pour tout reels x et y avec x différent de y vérifiant : xy=2 , l'inégalité suivante est vérifier :

( (x+y)² - 6) ((x-y)² + 8 ) >= k (x-y)²

Oty a écrit:: Trouver la valeur max de k tel que pour pour tout reels x et y avec x différent de y vérifiant : xy=2 , l'inégalité suivante est vérifier :
( (x+y)² - 6) ((x-y)² + 8 ) >= k (x-y)²

On a $Trouver K_{max} Gif$ .
D'autre part, on a selon l'inégalité arithmético-géométrique: 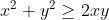$Trouver K_{max} Gif$ .
Et tenant compte que x et y sont différents, alors $Trouver K_{max} Gif$ .
On pose maintenant: $Trouver K_{max} Gif$ , ainsi $Trouver K_{max} Gif$ .
Notre inégalité devient alors $Trouver K_{max} Gif$ , ou encore $Trouver K_{max} Gif.latex?(t+2)(t+8 )\ge k$ .
On pose alors $Trouver K_{max} Gif$ .
Il s'agit d'un trinôme du second degré dont le discriminent est $Trouver K_{max} Gif$ .
Puisqu'on a $Trouver K_{max} Gif$ et le coefficient de 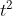$Trouver K_{max} Gif$ est strictement positif, il faut que son discriminent soit strictement négatif.
Cela est réalisé si et seulement si: $Trouver K_{max} Gif$ .
On tombe sur $Trouver K_{max} Gif$ (et un bonus $Trouver K_{max} Gif$ ).
Sauf erreurs.

oui exactement nmo c'est aussi ma solution , je vois que cette approche marche a merveille Hamdoullah Very Happy

. Il ne te reste qu'a prouver que l'inégalité est vrai pour k=18 .

» Comment trouver trouver f-1 ?
» TRouver a,b,c
» trouver les P
» trouver f
» trouver 3