- Oty a écrit:
- Resoudre dans Z : x²+y²=(x-y)^3 .
On a intérêt à résoudre
^3)
.
Si (x,y) est solution, alors on a absolument
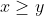
.
Maintenant, l'équation équivaut à
^3)
ou bien à
^2+(x-y)^2=2(x-y)^3)
.
Donc
^2=2(x-y)^3-(x-y)^2=(x-y)^2(2(x-y)-1))
.==>(*)
Cette égalité implique que
-1)
est un carré parfait impair.
Il existe donc un entier t tel que
-1=(2t+1)^2=4t^2+4t+1)
.
Et cela nous donne
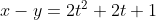
.
On reprend dans *, on trouve que
^2=(2t^2+2t+1)^2(2t+1)^2=\bigg((2t+1)(2t^2+2t+1)\bigg)^2)
.
Et ainsi
(2t^2+2t+1))
ou bien
(2t^2+2t+1))
.
On traite chacun des cas séparément:
***Le premier cas:
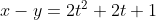
et
(2t^2+2t+1))
.
Et cela donne après quelques manipulations
(2t^2+2t+1))
et
)
.
La condition
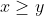
est satisfaite, car
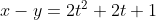
(un polynôme du second degré dont le discriminent est négatif qui garde un signe positif).
Le couple
=\bigg((t+1)(2t^2+2t+1),t(2t^2+2t+1)\bigg))
où t est un entier, est solution de l'équation proposée.
***Le second cas:
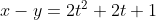
et
(2t^2+2t+1))
.
On trouve de même que
)
et que
(2t^2+2t+1))
.
On vérifie aisément que la condition
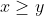
est satisfaite et que le couple
=\bigg(-t(2t^2+2t+1),-(t+1)(2t^2+2t+1)\bigg))
où t est un entier, est solution de l'équation proposée.
***Synthèse:
Si S était l'ensemble des solution de l'équation proposée, on aura donc:
(2t^2+2t+1),t(2t^2+2t+1)\bigg)/\text{t}\in\mathbb{Z}\}\bigcup\{\bigg(-t(2t^2+2t+1),-(t+1)(2t^2+2t+1)\bigg)/\text{t}\in\mathbb{Z}\})
.
Sauf erreurs.
