Simple Question

Maître Nombre de messages : 77 Age : 29 Date d'inscription : 03/12/2010

Bonjour tout le monde ,

Je me demande pourquoi les fonctions trigonométriques n'ont pas de limite quand x tend vers +oo , Normalement , dans une fonction sin ou cos le x peut prendre toute les valeurs , Donc pourquoi pas de limite en +oo , Merci !

c'est une fonction periodique !

Maître Nombre de messages : 77 Age : 29 Date d'inscription : 03/12/2010

Ouii , c vrai , j'ai oublié ce point . Merci beaucouup ! Very Happy

Maître Nombre de messages : 77 Age : 29 Date d'inscription : 03/12/2010

Donc , c pourquoi il n'admette de limite que dans des points ?

IMANE1 a écrit:: Bonjour tout le monde ,

Je me demande pourquoi les fonctions trigonométriques n'ont pas de limite quand x tend vers +oo , Normalement , dans une fonction sin ou cos le x peut prendre toute les valeurs , Donc pourquoi pas de limite en +oo , Merci !

Cela se démontre:

Lemme: Soit f une fonction périodique de période T>0, on suppose que: $Simple Question Gif$ . Donc la fonction f est constante.

Preuve 1: Montrons que: $Simple Question Gif$ .
Par l'absurde, on suppose que: $Simple Question Gif$ (et que aussi $Simple Question Gif$ ).
On a: $Simple Question Gif$ , alors:
$Simple Question Gif$ .
On prends: $Simple Question Gif$ , il s'en suit que:
$Simple Question Gif$ .
f est T-périodique, donc: $Simple Question Gif.latex?(\forall%20n\in%20\mathbb{Z}):%20f(a+n$ .
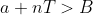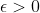On choisit un entier relatif n suffisamment large tel que: $Simple Question Gif$ (Par exemple: $Simple Question Gif$ ou bien $Simple Question Gif.latex?n=E(\frac{B-a}{T})+999..$ rabbit

).
Donc: $Simple Question Gif$ ou: $Simple Question Gif$ : ABSURDE !
D'où: $Simple Question Gif$ .

Preuve 2:
Soit: $Simple Question Gif$ , on a: $Simple Question Gif$ . Donc:
$Simple Question Gif$ .
Soient a et b deux réels , il existe k et h de Z tel que: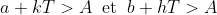
$Simple Question Gif$ . Alors:
$Simple Question Gif$ ou: $Simple Question Gif$ (f est T-périodique).
Et on a d'après l'inégo triangulaire:
$Simple Question Gif$ .
On fait tendre epsilon vers 0, et on obtient f(a)=f(b). Cela implique que f est constante.

Preuve 3: pour tt entier relatif n on a: f(x+nT)=f(x).
On a: $Simple Question Gif$ et: $Simple Question Gif$ (X=x+nT)
Donc: $Simple Question Gif$ .

Revenons au problème:
Puisque la fonction cos est une fonction périodique et non-constante, on déduit d'après le lemme démontré que cette fonction n'admet pas une limite finie en +oo (ni dans -oo).
Et puisque pour tout réel x: -1=< cos(x)=< 1, on conclut que cos n'admet pas une limite infinie, et il résulte qu'elle n'admet pas une limite en +oo (ni dans -oo). Et la même chose pour la fonction sinus...

ali-mes a écrit:

IMANE1 a écrit:: Bonjour tout le monde ,

Je me demande pourquoi les fonctions trigonométriques n'ont pas de limite quand x tend vers +oo , Normalement , dans une fonction sin ou cos le x peut prendre toute les valeurs , Donc pourquoi pas de limite en +oo , Merci !

Cela se démontre:

Lemme: Soit f une fonction périodique de période T>0, on suppose que: $Simple Question Gif$ . Donc la fonction f est constante.

Preuve 1: Montrons que: $Simple Question Gif$ .
Par l'absurde, on suppose que: $Simple Question Gif$ (et que aussi $Simple Question Gif$ ).
On a: $Simple Question Gif$ , alors:
$Simple Question Gif$ .
On prends: $Simple Question Gif$ , il s'en suit que:
$Simple Question Gif$ .
f est T-périodique, donc: $Simple Question Gif.latex?(\forall%20n\in%20\mathbb{Z}):%20f(a+n$ .
On choisit un entier relatif n suffisamment large tel que: 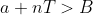$Simple Question Gif$ (Par exemple: $Simple Question Gif$ ou bien $Simple Question Gif.latex?n=E(\frac{B-a}{T})+999..$ rabbit

).
Donc: $Simple Question Gif$ ou: $Simple Question Gif$ : ABSURDE !
D'où: $Simple Question Gif$ .

Preuve 2:
Soit: 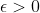$Simple Question Gif$ , on a: $Simple Question Gif$ . Donc:
$Simple Question Gif$ .
Soient a et b deux réels , il existe k et h de Z tel que:
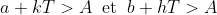$Simple Question Gif$ . Alors:
$Simple Question Gif$ ou: $Simple Question Gif$ (f est T-périodique).
Et on a d'après l'inégo triangulaire:
$Simple Question Gif$ .
On fait tendre epsilon vers 0, et on obtient f(a)=f(b). Cela implique que f est constante.

Preuve 3: pour tt entier relatif n on a: f(x+nT)=f(x).
On a: $Simple Question Gif$ et: $Simple Question Gif$ (X=x+nT)
Donc: $Simple Question Gif$ .

Revenons au problème:
Puisque la fonctions cos est une fonction périodique et non-constantes, on déduit d'après le lemme démontré que cette fonction n'admet pas une limite finie en +oo (ni dans -oo).
Et puisque pour tout réel x: -1=< cos(x)=< 1, on conclut que cos n'admet pas une limite infinie, et il résulte qu'elle n'admet pas une limite en +oo (ni dans -oo). Et la même chose pour la fonction sinus...

belle démonstration Cool

Maître Nombre de messages : 77 Age : 29 Date d'inscription : 03/12/2010

MERCI

» question (simple)!
» Aide
» l'été SM : Le GraNd jEu ...
» Simple !
» un simple exo