younesmath2012---2

personne n'a encore trouver une solution

àui personne !!!

est ce que Mr ''oty'' a une idee pour celle ci !!!!!!

cette inégalité n'est pas difficile , mais comme personne ne participe ;
Voici ma solution : Par AM-GM
en posant x=a\b , y=b\c , z=c\a ; il suffit de montrer que : pour xyz=1 , qui est un résultat tres connue et deja posté sur le forum ....

pourquoi on a un peut de detail svp!!!!!!

younesmath2012 a écrit:

pourquoi on a un peut de detail svp!!!!!!

mais c'est juste '' power-mean AM-GM '' .
Si r > s alors :
[img]http://latex.codecogs.com/gif.latex?\sqrt[r]{\frac{\sum&space;x_{i}^{r}}{n}}&space;\geq&space;\sqrt[s]{\frac{\sum&space;x_{i}^s}{n}}[/img]

si on utilise power-mean AM-GM on ne trouvera pas verifie stp!!!

oui j'ai oublier un cube faute de frappe voila :
sa ne change pas la suite de la démo

Oty a écrit:

cette inégalité n'est pas difficile , mais comme personne ne participe ;
Voici ma solution : Par AM-GM
en posant x=a\b , y=b\c , z=c\a ; il suffit de montrer que : pour xyz=1 , qui est un résultat tres connue et deja posté sur le forum ....

c'est pas juste il faut poser x=b/a ; y=c/b ; z=a/c pour trover votre relation

fin tposta fl forume svp???

younesmath2012 a écrit:

fin tposta fl forume svp???

essayer de la démontrer elle est intéressante je me rappelle plus fine t7atate .. (t7atate fe 4 variable mais je me rappel plus fine )

younesmath2012 a écrit:

Voici ma solution pour cette inégalité au cas où .
Lemme:
Soient a, b et c trois réels strictement positifs.
On a .
Preuve:
Cette inégalité équivaut à , ce qui est l'inégalité de Schur au cas où t=1.

On doit démontrer que , soit .
On pose .
De même, on définit et 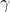cycliquement.
Il est clair qu'on a .
On pose encore une fois , donc .
De même, on définit y et z cycliquement.
On pose pour la dernière fois , et .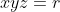
La condition conduit à .
Ce qui devient en utilisant les nouvelles notations: .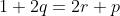
Selon le second lemme, on peut écrire .
Et il suffirait ainsi de démontrer que .
Et puisque 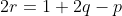, cette dernière inégalité devient .
Or, on a selon un théorème très connu donc .
Et on aura par conséquent .
Et il suffit encore de démontrer que .
On définit la fonction réelle f par .
Cette fonction a pour dérivée le trinôme négatif .
Et cela veut dire que f est décroissante sur .
On a selon le premier lemme , soit .
Donc ou bien et finalement .
Et puisque f est décroissante, il résulte que .
C'est à dire que .
On vient donc de démontrer que et le cas d'égalité est bel et bien lorsque les trois variables sont égaux.
CQFD.
Sauf erreurs.

@nmo le premier lemme est faux ! a=0 , b=1 , c=3 : LHS= 1+ 1\4 < 3\2 (cette inégalité est cyclic tu peux pas assumer a >=b>=c )

votre lemme1 est totalement faux!!!!!

Oty a écrit:

@nmo le premier lemme est faux ! a=0 , b=1 , c=3 : LHS= 1+ 1\4 < 3\2 (cette inégalité est cyclic tu peux assumer a >=b>=c )

Est ce qu'il existe un autre contre exemple où les variables ne sont pas nuls?
Oui j'ai trouvé que , et j'ai douté... As-t-on cette inégalité? N'est-elle pas une conséquence de l'inégalité de réordonnement?
Je vais réfléchir encore une fois.

non l'inégalité est cyclique tu ne peux ordonné les variable a moins de distinguer deux cas :
a>=b>=c et a>=c>=b . Pour a=1 , b=2 , c=4 LHS=1\3 + 2\6 + 4\5 < 3\2

younesmath2012 a écrit:

fin tposta fl forume svp???

bon voici ma solution pour l'inégalité restante :
par C-S :
il s'ensuit que :

ainsi il suffit de prouver que :

l'inégalité est démontré .

Oty a écrit:

younesmath2012 a écrit:

fin tposta fl forume svp???

bon voici ma solution pour l'inégalité restante :
par C-S :
il s'ensuit que :

ainsi il suffit de prouver que :

l'inégalité est démontré .

Il est belle cet astuce . BRAVO

bravo 3lik tani 3la had la9ta!!!bravo!!!

Merci beaucoup c'est juste une manipulation de C-S . Au plaisir .

Oty a écrit:

non l'inégalité est cyclique tu ne peux ordonné les variable a moins de distinguer deux cas :
a>=b>=c et a>=c>=b . Pour a=1 , b=2 , c=4 LHS=1\3 + 2\6 + 4\5 < 3\2

Oui tu as raison. J'ai commis une grave erreur de calcul.
Au lieu d'obtenir , je me suis perdu à côté de .
(Je n'ai pas voulu supprimer mon message car il contient des trucs intéressants).
Merci pour ta solution et l'évaluation de ma solution.