|
| | partie entiere |  |
| | | Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: partie entiere Sujet: partie entiere  Mer 29 Aoû 2012, 11:49 Mer 29 Aoû 2012, 11:49 | |
| montrer que 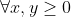 on a +E(5y)\geq%20E(3x+y)+E(x+3y)) c.a.d (l'autre notation) [img]http://latex.codecogs.com/gif.latex?\left%20[%205x%20\right%20]+\left%20[%205y%20\right%20]\geq%20\left%20[%203x+y%20\right%20]+\left%20[%20x+3y%20\right%20][/img] | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Mer 29 Aoû 2012, 15:39 Mer 29 Aoû 2012, 15:39 | |
|
Dernière édition par Mohammed_Lahlou le Dim 02 Déc 2012, 15:00, édité 2 fois | |
|   | | younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Mer 29 Aoû 2012, 15:46 Mer 29 Aoû 2012, 15:46 | |
| on a x,y 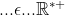 | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Mer 29 Aoû 2012, 15:48 Mer 29 Aoû 2012, 15:48 | |
| - younesmath2012 a écrit:
- on a x,y
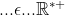 Tu devais faire une faute de frappe, ce n'est rien dans tout les cas, ma réponse est-elle juste ? | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Jeu 30 Aoû 2012, 15:20 Jeu 30 Aoû 2012, 15:20 | |
| E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
3E(x)+E(y)=<3x+y<3E(x)+E(y)+(3r+s)/5
E(x)+3E(y)=<x+3y<E(x)+3E(y)+(r+3s)/5
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
E(3x+y)+E(x+3y)=<E(5x)+E(5y)
si 4E(x)+4E(y)+u+v=<5E(x)+r+5E(y)+s
si u+v=<E(x)+E(y)+r+s
ce qui est vrai car u+v=<r+s et x,y>=0
| |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Jeu 30 Aoû 2012, 15:29 Jeu 30 Aoû 2012, 15:29 | |
| EXTENSION POSSIBLE
x,y > 0 et a,b,c >0 avec a>=b+c alors E(ax)+E(ay)>= E(c x+by)+E(bx+c y) | |
|   | | younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Jeu 30 Aoû 2012, 17:19 Jeu 30 Aoû 2012, 17:19 | |
| - abdelbaki.attioui a écrit:
- E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
3E(x)+E(y)=<3x+y<3E(x)+E(y)+(3r+s)/5
E(x)+3E(y)=<x+3y<E(x)+3E(y)+(r+3s)/5
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
E(3x+y)+E(x+3y)=<E(5x)+E(5y)
si 4E(x)+4E(y)+u+v=<5E(x)+r+5E(y)+s
si u+v=<E(x)+E(y)+r+s
ce qui est vrai car u+v=<r+s et x,y>=0
votre reponse Mr "abdelbaki.attioui" est logique sauf la derniere ligne qui n'est pas clair car il faut montrer que: u+v=<E(x)+E(y)+r+s ''ce qui est vrai car u+v=<r+s et x,y>=0'' ce qui est en rouge n'est pas toujours juste !!!!!! il faut donc MQ:u+v=<E(x)+E(y)+r+s pour que votre reponse soit complete!!!! et excuser moi!!!! | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Jeu 30 Aoû 2012, 20:34 Jeu 30 Aoû 2012, 20:34 | |
| - younesmath2012 a écrit:
- abdelbaki.attioui a écrit:
- E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
3E(x)+E(y)=<3x+y<3E(x)+E(y)+(3r+s)/5
E(x)+3E(y)=<x+3y<E(x)+3E(y)+(r+3s)/5
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
E(3x+y)+E(x+3y)=<E(5x)+E(5y)
si 4E(x)+4E(y)+u+v=<5E(x)+r+5E(y)+s
si u+v=<E(x)+E(y)+r+s
ce qui est vrai car u+v=<r+s et x,y>=0
votre reponse Mr "abdelbaki.attioui" est logique sauf la derniere ligne qui n'est pas clair car il faut montrer que:
u+v=<E(x)+E(y)+r+s ''ce qui est vrai car u+v=<r+s et x,y>=0''
ce qui est en rouge n'est pas toujours juste !!!!!!
il faut donc MQ:u+v=<E(x)+E(y)+r+s pour que votre reponse soit complete!!!! et excuser moi!!!! Vous n'avez pas bien lu la solution !!! u+v=<(3r+s)/5 + (r+3s)/5= 4(r+s) / 5 =< r+s =< E(x)+E(y)+r+s | |
|   | | younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Ven 31 Aoû 2012, 12:16 Ven 31 Aoû 2012, 12:16 | |
| - abdelbaki.attioui a écrit:
- E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
3E(x)+E(y)=<3x+y<3E(x)+E(y)+(3r+s)/5
E(x)+3E(y)=<x+3y<E(x)+3E(y)+(r+3s)/5
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
E(3x+y)+E(x+3y)=<E(5x)+E(5y)
si 4E(x)+4E(y)+u+v=<5E(x)+r+5E(y)+s
si u+v=<E(x)+E(y)+r+s
ce qui est vrai car u+v=<r+s et x,y>=0
ah bon!!! excuser moi!!! j'ai pas vu ce qui est en vert pouvez vous expliquer pourquoi on a 0=<u=<(3r+s)/5 et u entier et 0=<v=<(r+3s)/5 et v entiermerci d'avance !!!! | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Ven 31 Aoû 2012, 12:49 Ven 31 Aoû 2012, 12:49 | |
| E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
===> 5E(x)+r=<5x<5E(x)+r+1 et 5E(y)+s=<5y<5E(y)+s+1
===> 3E(x)+E(y)+(3r+s)/5=<3x+y< 3E(x)+E(y)+(3r+s)/5+4/5
de même E(x)+3E(y)+(r+3s)/5=<x+3y< E(x)+3E(y)+(r+3s)/5+4/5
alors
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
En fait u= E((3r+s)/5) et v=E((r+3s)/5)
car E est croissante et E(x+n)=E(x)+n qqs x réel et n dans Z | |
|   | | younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Ven 31 Aoû 2012, 13:26 Ven 31 Aoû 2012, 13:26 | |
| - abdelbaki.attioui a écrit:
- E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
===> 5E(x)+r=<5x<5E(x)+r+1 et 5E(y)+s=<5y<5E(y)+s+1
===> 3E(x)+E(y)+(3r+s)/5=<3x+y< 3E(x)+E(y)+(3r+s)/5+4/5
de même E(x)+3E(y)+(r+3s)/5=<x+3y< E(x)+3E(y)+(r+3s)/5+4/5
alors
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
En fait u= E((3r+s)/5) et v=E((r+3s)/5)
car E est croissante et E(x+n)=E(x)+n qqs x réel et n dans Z POURQUOI u= E((3r+s)/5) et v=E((r+3s)/5) ? !!! | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Ven 31 Aoû 2012, 16:51 Ven 31 Aoû 2012, 16:51 | |
| - younesmath2012 a écrit:
- abdelbaki.attioui a écrit:
- E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
===> 5E(x)+r=<5x<5E(x)+r+1 et 5E(y)+s=<5y<5E(y)+s+1
===> 3E(x)+E(y)+(3r+s)/5=<3x+y< 3E(x)+E(y)+(3r+s)/5+4/5
de même E(x)+3E(y)+(r+3s)/5=<x+3y< E(x)+3E(y)+(r+3s)/5+4/5
alors
E(3x+y)=3E(x)+E(y)+u avec 0=<u=<(3r+s)/5 et u entier
E(x+3y)=E(x)+3E(y)+v avec 0=<v=<(r+3s)/5 et v entier
En fait u= E((3r+s)/5) et v=E((r+3s)/5)
car E est croissante et E(x+n)=E(x)+n qqs x réel et n dans Z POURQUOI u= E((3r+s)/5) et v=E((r+3s)/5) ? !!! Bien vu Younes effectivement u= E((3r+s)/5) si 3r+s=<1 3r+s+1=5q+t et r+3s+1=5q'+t' ( Division euclidienne) ==> 3E(x)+E(y)+q+(t-1)/5=<3x+y< 3E(x)+E(y)+q+1/5 ==> E(3x+y)=3E(x)+E(y)+q de même E(x+3y)=E(x)+3E(y)+q' | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Dim 02 Sep 2012, 01:15 Dim 02 Sep 2012, 01:15 | |
| E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
5E(x)+r=<5x<5E(x)+r+1 et 5E(y)+s=<5y<5E(y)+s+1
3E(x)+E(y)+(3r+s)/5=< 3x+y< 3E(x)+E(y)+(3r+s+4)/5 ---->(1)
E(x)+3E(y)+(r+3s)/5=< x+3y< E(x)+3E(y)+(r+3s+4)/5 -----> (2)
Par symétrie on suppose r=<s
si r+s=<1 ==> r=0 et s=<1
(1) ==> 3E(x)+E(y)+s/5=< 3x+y< 3E(x)+E(y)+(s+4)/5 =<3E(x)+E(y)+1
==> E(3x+y)=3E(x)+E(y)
(2) ==> E(x)+3E(y)+3s/5=< x+3y< E(x)+3E(y)+(3s+4)/5 =< E(x)+3E(y)+s+1
==> E(x+3y)=<E(x)+3E(y)+s
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+s=< E(5x)+E(5y) car x,y>=0 ==> E(x) et E(y)>=0
si r+s=2
si r=0 et s=2
(1) ==> 3E(x)+E(y)+2/5=< 3x+y< 3E(x)+E(y)+6/5
==> E(3x+y)=<3E(x)+E(y)+1
(2) ==> E(x)+3E(y)+6/5=< x+3y< E(x)+3E(y)+2
==> E(x+3y)=E(x)+3E(y)+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+2=< E(5x)+E(5y)
si r=s=1
(1) ==> 3E(x)+E(y)+4/5=< 3x+y< 3E(x)+E(y)+8/5
==> E(3x+y)=<3E(x)+E(y)+1
(2) ==> E(x)+3E(y)+4/5=< x+3y< E(x)+3E(y)+8/5
==> E(x+3y)=<E(x)+3E(y)+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+2=< E(5x)+E(5y)
si r+s=>3
(1) et (2) ==> E(3x+y)+ E(x+3y)< 4E(x)+4E(y) +4(r+s+2)/5 =<4E(x)+4E(y)+r+s+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+r+s=< E(5x)+E(5y)
En fait on a montré que E(3x+y)+ E(x+3y)+E(x)+E(y)=< E(5x)+E(5y)
| |
|   | | younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Lun 03 Sep 2012, 14:58 Lun 03 Sep 2012, 14:58 | |
| [quote="abdelbaki.attioui"]E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
5E(x)+r=<5x<5E(x)+r+1 et 5E(y)+s=<5y<5E(y)+s+1
3E(x)+E(y)+(3r+s)/5=< 3x+y< 3E(x)+E(y)+(3r+s+4)/5 ---->(1)
E(x)+3E(y)+(r+3s)/5=< x+3y< E(x)+3E(y)+(r+3s+4)/5 -----> (2)
Par symétrie on suppose r=<s
si r+s=<1 ==> r=0 et s=<1
(1) ==> 3E(x)+E(y)+s/5=< 3x+y< 3E(x)+E(y)+(s+4)/5 =<3E(x)+E(y)+1
==> E(3x+y)=3E(x)+E(y)
(2) ==> E(x)+3E(y)+3s/5=< x+3y< E(x)+3E(y)+(3s+4)/5 =< E(x)+3E(y)+s+1
==> E(x+3y)=<E(x)+3E(y)+s
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+s=< E(5x)+E(5y) car x,y>=0 ==> E(x) et E(y)>=0
si r+s=2
si r=0 et s=2
(1) ==> 3E(x)+E(y)+2/5=< 3x+y< 3E(x)+E(y)+6/5
==> E(3x+y)=<3E(x)+E(y)+1
(2) ==> E(x)+3E(y)+6/5=< x+3y< E(x)+3E(y)+2
==> E(x+3y)=E(x)+3E(y)+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+2=< E(5x)+E(5y)
si r=s=1
(1) ==> 3E(x)+E(y)+4/5=< 3x+y< 3E(x)+E(y)+8/5
==> E(3x+y)=<3E(x)+E(y)+1
(2) ==> E(x)+3E(y)+4/5=< x+3y< E(x)+3E(y)+8/5
==> E(x+3y)=<E(x)+3E(y)+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+2=< E(5x)+E(5y)
si r+s=>3
(1) et (2) ==> E(3x+y)+ E(x+3y)< 4E(x)+4E(y) +4(r+s+2)/5 =<4E(x)+4E(y)+r+s+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+r+s=< E(5x)+E(5y)
En fait on a montré que E(3x+y)+ E(x+3y)+E(x)+E(y)=< E(5x)+E(5y) /quote]
salut Mr "abdelbaki.attioui" je crois que le symbolle < n'est pas clair!!! il faut le justifier car normalement en passant a la fonction E on aura
E(3x+y)+ E(x+3y)=< 4E(x)+4E(y) +4(r+s+2)/5 =<4E(x)+4E(y)+r+s+1 donc la solution n'est pas terminé n'est ce pas MR "abdelbaki.attioui" ? | |
|   | | abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Lun 03 Sep 2012, 15:28 Lun 03 Sep 2012, 15:28 | |
| [quote="younesmath2012"] - abdelbaki.attioui a écrit:
- E(5x)=5E(x)+r et E(5y)=5E(y)+s avec (r,s) dans {0,1,2,3,4}X{0,1,2,3,4}
5E(x)+r=<5x<5E(x)+r+1 et 5E(y)+s=<5y<5E(y)+s+1
3E(x)+E(y)+(3r+s)/5=< 3x+y< 3E(x)+E(y)+(3r+s+4)/5 ---->(1)
E(x)+3E(y)+(r+3s)/5=< x+3y< E(x)+3E(y)+(r+3s+4)/5 -----> (2)
Par symétrie on suppose r=<s
si r+s=<1 ==> r=0 et s=<1
(1) ==> 3E(x)+E(y)+s/5=< 3x+y< 3E(x)+E(y)+(s+4)/5 =<3E(x)+E(y)+1
==> E(3x+y)=3E(x)+E(y)
(2) ==> E(x)+3E(y)+3s/5=< x+3y< E(x)+3E(y)+(3s+4)/5 =< E(x)+3E(y)+s+1
==> E(x+3y)=<E(x)+3E(y)+s
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+s=< E(5x)+E(5y) car x,y>=0 ==> E(x) et E(y)>=0
si r+s=2
si r=0 et s=2
(1) ==> 3E(x)+E(y)+2/5=< 3x+y< 3E(x)+E(y)+6/5
==> E(3x+y)=<3E(x)+E(y)+1
(2) ==> E(x)+3E(y)+6/5=< x+3y< E(x)+3E(y)+2
==> E(x+3y)=E(x)+3E(y)+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+2=< E(5x)+E(5y)
si r=s=1
(1) ==> 3E(x)+E(y)+4/5=< 3x+y< 3E(x)+E(y)+8/5
==> E(3x+y)=<3E(x)+E(y)+1
(2) ==> E(x)+3E(y)+4/5=< x+3y< E(x)+3E(y)+8/5
==> E(x+3y)=<E(x)+3E(y)+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+2=< E(5x)+E(5y)
si r+s=>3
(1) et (2) ==> E(3x+y)+ E(x+3y)< 4E(x)+4E(y) +4(r+s+2)/5 =<4E(x)+4E(y)+r+s+1
==> E(3x+y)+ E(x+3y)=< 4E(x)+4E(y)+r+s=< E(5x)+E(5y)
En fait on a montré que E(3x+y)+ E(x+3y)+E(x)+E(y)=< E(5x)+E(5y) /quote]
salut Mr "abdelbaki.attioui" je crois que le symbolle < n'est pas clair!!! il faut le justifier car normalement en passant a la fonction E on aura
E(3x+y)+ E(x+3y)=< 4E(x)+4E(y) +4(r+s+2)/5 =<4E(x)+4E(y)+r+s+1 donc la solution n'est pas terminé n'est ce pas MR "abdelbaki.attioui" ? J'ai pensé que ce n'est pas la peine d'écrire ceci mais voilà E(3x+y)+ E(x+3y)=< (3x+y)+(x+3y)< 4E(x)+4E(y) +4(r+s+2)/5 =<4E(x)+4E(y)+r+s+1 On ne passe pas par E pour garder < de (1) et (2) . La solution est achevée et s'il y en a d' autres je serais ravis de les lire
Dernière édition par abdelbaki.attioui le Lun 03 Sep 2012, 15:44, édité 1 fois | |
|   | | younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  Lun 03 Sep 2012, 15:42 Lun 03 Sep 2012, 15:42 | |
| safi daba la solution est complete
bravo Mr "abdelbaki.attioui" vous avez bien detaille votre solution!!!
merci bien !!! | |
|   | | Contenu sponsorisé
 |  Sujet: Re: partie entiere Sujet: Re: partie entiere  | |
| |
|   | | | | partie entiere |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
