| | own(younesmath2012) |  |
|
|
| Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: own(younesmath2012) Sujet: own(younesmath2012)  Ven 07 Sep 2012, 19:46 Ven 07 Sep 2012, 19:46 | |
| 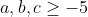 tq 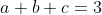 MQ: (a-2)}{a^{2}+3}+\frac{(b-1)(b-2)}{b^{2}+3}+\frac{(c-1)(c-2)}{c^{2}+3}\geq%200) il ya une simple methode pour repondre !!!!!! | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Dim 09 Sep 2012, 21:11 Dim 09 Sep 2012, 21:11 | |
| Je propose ma solution ,sans utiliser le faite que a,b,c>=-5 l’idée est d'utiliser l'inégalité de Chebyshev avec (a-1)+(b-1)+(c-1) ainsi on aura un coté nul chose qui permettra de conclure par symétrie supposons que a=<b=<c donc a-1=<b-1=<c-1 et donc pour appliquer la méthode il suffit de prouver que:  ou bien monter que la fonction: =\frac{x-2}{x^2+3}) est croissante , chose qui est vrai seulement pour  cela nous convient puisque l'inégalité est trivial si [img]http://latex.codecogs.com/gif.latex?x\in&space;]-\infty&space;,2-\sqrt{7}]\cup&space;[2+\sqrt{7},+\infty&space;[/img] il ne reste plus qu'applique Chebyshev, on aura (\sum&space;\frac{a-2}{a^2+3})\leq&space;\sum&space;\frac{(a-1)(a-2)}{a^2+3}\Leftrightarrow&space;\sum&space;\frac{(a-1)(a-2)}{a^2+3}\geq&space;0) | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 11:12 Lun 10 Sep 2012, 11:12 | |
| C simple avec l inégalité de jensen | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 13:13 Lun 10 Sep 2012, 13:13 | |
| puisque ''C simple avec l inégalité de jensen'' comme vous avez dit alors tu peut poster votre reponse complete !!!
on attend votre reponse Mr''Yassirhassininador'' !!! | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 13:23 Lun 10 Sep 2012, 13:23 | |
| | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 13:25 Lun 10 Sep 2012, 13:25 | |
| jusqu'a maintenant personne n'a donné la bonne repose ( elle est simple) | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 13:39 Lun 10 Sep 2012, 13:39 | |
| On pose f(x)=(x-1)(x-2)/(x^2+1) .
D après linegalite de je s'en on a :
1/3 S > (a+b+c/3-1)(a+b+c/3-2)/((a+b+c/3)^2 +1)=0 | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 13:54 Lun 10 Sep 2012, 13:54 | |
| c'est faux la fonction n'est pas totalement convexe . Bon alors voici ma solution : c'est equivalent a : \sum (a-1)²\a²+3 >= \sum a-1\a²+3 cette ecriture montre qu'il suffit de prouver que le membre de droite est négatif ou encore \sum 1-a \ a²+3 >=0 , assumant a>=b>=c , par chebichev puisque les suites (1-a,1-b,1-c) et (1\a²+3 , 1\b²+3 , 1\c²+3) sont dans le meme ordre alors \sum 1-a \a²+3 >= 1\3 (3-a-b-c) (\sum 1\a²+3) =0 .  | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 16:36 Lun 10 Sep 2012, 16:36 | |
| Oui je sait mais regarde la condition | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 16:37 Lun 10 Sep 2012, 16:37 | |
| Qui peut m'expliquer IAG pondère ? | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 18:18 Lun 10 Sep 2012, 18:18 | |
| - Oty a écrit:
- c'est faux la fonction n'est pas totalement convexe .
Bon alors voici ma solution :
c'est equivalent a :
\sum (a-1)²\a²+3 >= \sum a-1\a²+3
cette ecriture montre qu'il suffit de prouver que le membre de droite est négatif ou encore
\sum 1-a \ a²+3 >=0 , assumant a>=b>=c , par chebichev puisque les suites
(1-a,1-b,1-c) et (1\a²+3 , 1\b²+3 , 1\c²+3) sont dans le meme ordre alors
\sum 1-a \a²+3 >= 1\3 (3-a-b-c) (\sum 1\a²+3) =0 .
 MR''oty'' a bien expliquer sa reponse , bravo !!! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 22:05 Lun 10 Sep 2012, 22:05 | |
| Merci , Mr Younes , pouvez vous nous montrer votre solution ? Merci . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Lun 10 Sep 2012, 23:18 Lun 10 Sep 2012, 23:18 | |
| j'ai minoré par une fonction lineaire puis j'ai sommé
je vais poster ma solution quand j'aurait le temps aujourd'hui ou demain inchaallah | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Mar 11 Sep 2012, 00:06 Mar 11 Sep 2012, 00:06 | |
| on a (a-2)}{a^{2}+3}\geq%200\Leftrightarrow%20\sum%20\(1-\frac{3a+1}{a^{2}+3})\geq%200%20\Leftrightarrow%20\sum%20\frac{3a+1}{a^{2}+3}\leq%203\Leftrightarrow%20\sum%20f(a)\leq%203...avec...f(x)=%20\frac{3x+1}{x^{2}+3}...on...a...f(1)=1;f'(1)=\frac{1}{4}...on...va...minorer...par...g(x)=f(1)+f'(1)(x-1)=1+\frac{1}{4}(x-1)=\frac{x+3}{4}....pour%20...tout...x\geq%20-5...on...a...f(x)\leq%20g(x)...car...f(x)-g(x)=\frac{-x^3-3x^2+9x-5}{4(x^2+3)}=\frac{-(x+5)(x+1)^2}{4(x^2+3)}\leq%200) on a montré donc \leq%201+\frac{1}{4}(x-1)\Rightarrow%20\sum%20f(a)\leq%20\sum%20(1+\frac{1}{4}(a-1))=3+\frac{1}{4}(a+b+c-3)=3....termin%C3%A9) | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  Mar 11 Sep 2012, 00:53 Mar 11 Sep 2012, 00:53 | |
| vous pouvez faire la meme methode pour l'exercice suivant (polande 1996) [img]http://latex.codecogs.com/gif.latex?a,b,c\ge\frac{-3}{4}...tq....a+b+c=1....MQ:...\frac{a}{a^{2}+1}+\frac{b}{b^{2}+1}+\frac{c}{c^{2}+1}\le\frac{9}{10}[/img | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: own(younesmath2012) Sujet: Re: own(younesmath2012)  | |
| |
|
  | |
| | own(younesmath2012) |  |
|
