- H.O.A.B.C a écrit:
- Je commence Premier : Trouvez toutes les application F : C------>c tq f(z)+zf(1-z)=1+z . Bonne chance
Je propose une solution:
On a:
: f(z)+z.f(1-z)=1+z)
.
On effectue la tronsformation
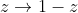
; on tombe sur
: f(1-z)+(1-z).f(z)=2-z)
, ou encore (en multiliant par z)
: z.f(1-z)+z(1-z).f(z)=2z-z^2)
.
En soustrayant la dernière équation de la première, on aura:
: f(z)(z-z^2-1)=z-z^2-1)
. ==>(*)
Appelons

l'une des solution de l'équation
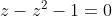
, alors
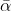
l'est aussi.
On déduit que
: f(z)=1)
selon *.
Et il est facile de vérifier que cette solution convient dans l'équation fonctionnelle.
On pose
=x)
et
=y)
en guise de simplification.
On aura le système suivant:
.x+y=2-\alpha\end{cases})
.
Le déterminant de ce système, le déterminant par rapport à x et le déterminant par rapport à y sont tous nuls.
Ce qui veut bien dire que le système admet une infinité de solution.
On pose
=x)
et
=y)
tels que
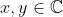
.
Finalement les solutions de l'équation fonctionnelle sont les application définies par:
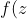=\begin{cases}1\,\,\,\,\text{si }z\in\mathbb{C}-\{\alpha,\bar{\alpha}\}\\f(\alpha)=x\,\,\,\,\,\,\,\, x\in\mathbb{C}\\f(\bar{\alpha})=y\,\,\,\,\,\,\,\, y\in\mathbb{C}\end{cases})
.
Sauf erreurs.
