voici ma solution que je me souviens avoir deja proposé quelque part ..., on a :
[img]http://latex.codecogs.com/gif.latex?f(a,b,c)-f(a,\frac{b+c}{2},\frac{b+c}{2})=81a[\frac{(b+c)^2}{4}(a^2+\frac{(b+c)^2}{2}))-bc(a^2+b^2+c^2))]=81a[a^{2}&space;\frac{(b-c)^{2}}{4}&space;+&space;\frac{(b+c)^4-8bc(b^2+c^2)}{8}]&space;=81a[a^{2}&space;\frac{(b-c)^{2}}{4}&space;+&space;\frac{(b-c)^4}{8}]&space;\geq&space;0[/img]
on pose t=(b+c)\2
il suffit de prouver que :
\geq&space;0&space;\Leftrightarrow&space;(a+2t)^5-81at^2&space;(a^2+2t^2)&space;\geq&space;0)
si a =0 l'inégalité est clairement vrai ;
pour a > 0 on pose z=t\a
l'inégalité est equivalente a :
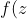=(1+2z)^5&space;-81z^2(1+2z^2)\geq&space;0&space;\Leftrightarrow&space;(z-1)^2&space;(32z^3-18z^2+12z+1)\geq&space;0)
ce qui est vrai , car

je pense que la meilleur solution est celle de Vasc l'inventeur de cette inégalité
en utilisant (ab+bc+ca)² >= 3abc(a+b+c)
puis on posant , p=a+b+c et q=ab+bc+ca sa donné une belle identité
