Difficile et jolie

Hamdoullah a khouya .
a sa7bi nta be douke les pdfs li kriti kamline ou baki la3alaka ,
le jolie a si alidos rahe 3la l'ef machi 3la la solution -_- bayna fike grand mathématicien ,
Mr Younesmaths bezzaf 3like tate wssel lihe nta a sa7bi 3ir mouta7achire fe hade forum kate 3ref 3ir te7fed 3amrek ma derti men rassek ga3e les solution li kate dire houma li kaynine fe Aops ou la lkitihoume fe chi pdf men les pdfs dialek .
n3awlou 3like hade 3ame mnine nta hadechi ki jike sahel , lkina lbatal dial maroc , alidos
7ssen like temchi tel3abe lbille .

, AOPS , PDF ,LBULLSHIT , ana 3aréfe Niveau dyali ! SO je préfères mantwlche M3ak !! 7ite li khsso ytgale rah tgale il y'a 14 minutes

En attendant OTy Ydir solution je Propose cette E.F !!

chnahouwa niveau dialek ?
Hade l'EF li 7atiti s3iba bezzaf elle demande des connaissances en ''construction '' , la kounti kate kder t7alha nta rassek rake ''pco 2 ''

Drari, machi haka rat3almo!!! rah 7na hna bach nstafdo machi bach wa7ed idor f wa7ed. Daba f 4 dial les pages dial discussions makayna tachi ma3louma ratnfa3e drari li taywajdo IMO!!!

o machi mochkil ila kane 9ari bzaf dial les pdfs, tbark allah 3lih...

MR Bel-jad5 , machi mouchkile lakane kari bezzaf dial les PDFs bsa7tou ou tbarkellah 3lihe ,
ana kane 3ref 7ajja wa7da I7tarime tou7tarame !!

bel_jad5 a écrit:

Drari, machi haka rat3almo!!! rah 7na hna bach nstafdo machi bach wa7ed idor f wa7ed. Daba f 4 dial les pages dial discussions makayna tachi ma3louma ratnfa3e drari li taywajdo IMO!!!

o machi mochkil ila kane 9ari bzaf dial les pdfs, tbark allah 3lih...

LA likay9ra bzaf d les PDF ki walo , bnadém li capable kaytzade b dakchi mén 3énde allah


de L'ironie quoi !!

Lakounte ana li Dalem ngoulha like devant tout le monde :
Sma7e lia a Alidos !

Oty a écrit:

chnahouwa niveau dialek ?
Hade l'EF li 7atiti s3iba bezzaf elle demande des connaissances en ''construction '' , la kounti kate kder t7alha nta rassek rake ''pco 2 ''

sa7bi daba nssa dakchi li golte o trjéle M3aya pour étre brillant Khssék T3lém Tkhdéme

o ana je suis près npartagi bcp de truc intéréssante b7al hadchi meme des cours et des astuces

car PCO mawsslche ghir b les notions de bases

ana comme j'ai dit je suis prét npartagé des livres riches f hadchi

alidos a écrit:

, AOPS , PDF ,LBULLSHIT , ana 3aréfe Niveau dyali ! SO je préfères mantwlche M3ak !! 7ite li khsso ytgale rah tgale il y'a 14 minutes

En attendant OTy Ydir solution je Propose cette E.F !!

Pour had L'EF il suffit de voir qu'il a une infinité de solution il en reste de tatonner avec une fonction réelle g définie sur IR* qui va satisfaire l'EF

d'ou f est de la forme , f(x) = g(x) - g(1/x)

Pour vous , MR Bel-jad 5 , moi je prepare pas pour l'IMO , je fais sa que par plaisir et par amour des Maths . Voila :
on a :
P(0,x) => f(f(x))=x+f(0)²=x+a² (*) (on pose a=f(0))
en ecrivant :
f(LHS)=f(RHS) on a d'apres (*) :
xf(x)+y+a²=f(f(x)²+y)(**) on prend y=0 dans cette derniere on obtient :
xf(x)+a+a²=f(f(x)²) en remplace dans (**)
on obtient :
f(f(x)²+y)=f(f(x)²)+f(y)-a (I) quelque soit x et y dans R+ .
mais comme f(f(x))=x+a² cella donne que f est surjective pour tout nombre >= a² et donc tout nombre >= a^4 peut s'ecrire sous la forme f(z)² et donc de (I) on déduit que :
f(x+y)=f(x)+f(y)-a quelque soit x >= a^4 et quelque soit y>=0
on pose maintenant g(x)=f(x)-a d'apres la derniere relation on a bien
g(x+y)=g(x)+g(y) quelque soit x >= a^4 et quelque soit y>=0 .
on a alors :

g(a^4 +x+y)=g(a^4+x)+g(y)=g(a^4)+g(x)+g(y) pour tout x ,y >=0 et on a aussi
g(a^4+x+y)=g(a^4)+g(x+y) pour touut x,y >=0
en combinant c'est deux relation on obtient :
g(x+y)=g(x)+f(y) quelque soit x et y >=0
et comme pour tout x g(x)>= - a , ainsi Caushy nous donne g(x)=cx et donc f(x)=cx+a , la reciproque nous donne
c=1 et b=0 (car f(x) >=0 ) et donc finalement
f(x)=x pour tout x >=0 .
sauf erreur ....

alidos a écrit:

sa7bi daba nssa dakchi li golte o trjéle M3aya pour étre brillant Khssék T3lém Tkhdéme

khouya je veux pas etre brillant , koule wa7ed ou tariktou kifache ki t3allem machi darouri khedma bezzaf .
Mouhime oublions hadechi matra walu , sma7e lia lakounte dlemtek .

Oty a écrit:

Pour vous , MR Bel-jad 5 , moi je prepare pas pour l'IMO , je fais sa que par plaisir et par amour des Maths . Voila :
on a :
P(0,x) => f(f(x))=x+f(0)²=x+a² (*) (on pose a=f(0))
en ecrivant :
f(LHS)=f(RHS) on a d'apres (*) :
xf(x)+y+a²=f(f(x)²+y)(**) on prend y=0 dans cette derniere on obtient :
xf(x)+a+a²=f(f(x)²) en remplace dans (**)
on obtient :
f(f(x)²+y)=f(f(x)²)+f(y)-a (I) quelque soit x et y dans R+ .
mais comme f(f(x))=x+a² cella donne que f est surjective pour tout nombre >= a² et donc tout nombre >= a^4 peut s'ecrire sous la forme f(z)² et donc de (I) on déduit que :
f(x+y)=f(x)+f(y)-a quelque soit x >= a^4 et quelque soit y>=0
on pose maintenant g(x)=f(x)-a d'apres la derniere relation on a bien
g(x+y)=g(x)+g(y) quelque soit x >= a^4 et quelque soit y>=0 .
on a alors :

g(a^4 +x+y)=g(a^4+x)+g(y)=g(a^4)+g(x)+g(y) pour tout x ,y >=0 et on a aussi
g(a^4+x+y)=g(a^4)+g(x+y) pour touut x,y >=0
en combinant c'est deux relation on obtient :
g(x+y)=g(x)+f(y) quelque soit x et y >=0
et comme pour tout x g(x)>= - a , ainsi Caushy nous donne g(x)=cx et donc f(x)=cx+a , la reciproque nous donne
c=1 et b=0 (car f(x) >=0 ) et donc finalement
f(x)=x pour tout x >=0 .
sauf erreur ....

t'as pas le droit de faire l'équation de cauchy ghir hakkak ( amicalement , O SM7liya o je demandes pardon l ga3 li 3ayrthome !!

Next exo , machi s3ibe bzaf !!!

c'est le cas ou g est Minoré et Monotone (par injectivité de f ) de l'equation de Cauchy , tu peux faire des recherches ...

ah ok tant qu'il est strictement Monotone c'est bon

Oty a écrit:

Pour vous , MR Bel-jad 5 , moi je prepare pas pour l'IMO , je fais sa que par plaisir et par amour des Maths . Voila :
on a :
P(0,x) => f(f(x))=x+f(0)²=x+a² (*) (on pose a=f(0))
en ecrivant :
f(LHS)=f(RHS) on a d'apres (*) :
xf(x)+y+a²=f(f(x)²+y)(**) on prend y=0 dans cette derniere on obtient :
xf(x)+a+a²=f(f(x)²) en remplace dans (**)
on obtient :
f(f(x)²+y)=f(f(x)²)+f(y)-a (I) quelque soit x et y dans R+ .
mais comme f(f(x))=x+a² cella donne que f est surjective pour tout nombre >= a² et donc tout nombre >= a^4 peut s'ecrire sous la forme f(z)² et donc de (I) on déduit que :
f(x+y)=f(x)+f(y)-a quelque soit x >= a^4 et quelque soit y>=0
on pose maintenant g(x)=f(x)-a d'apres la derniere relation on a bien
g(x+y)=g(x)+g(y) quelque soit x >= a^4 et quelque soit y>=0 .
on a alors :
g(a^4 +x+y)=g(a^4+x)+g(y)=g(a^4)+g(x)+g(y) pour tout x ,y >=0 et on a aussi
g(a^4+x+y)=g(a^4)+g(x+y) pour touut x,y >=0
en combinant c'est deux relation on obtient :
g(x+y)=g(x)+f(y) quelque soit x et y >=0
et comme pour tout x g(x)>= - a , ainsi Caushy nous donne g(x)=cx et donc f(x)=cx+a , la reciproque nous donne
c=1 et b=0 (car f(x) >=0 ) et donc finalement
f(x)=x pour tout x >=0 .
sauf erreur ....

Pour ce qui est en rouge, je ne sais pas comment tu t'es débarassé de la contrainte sur x?
Il était strictement supérieur à un certain 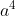, et puis tu as étendu la relation pour tous les réels positifs!!!

Oty a écrit:

Trouver toutes les fonctions définie de R+ vers R+ vérifiant l'équation suivante :

Je propose une solution:
On a .
On pose , l'équation fonctionnelle devient: .
Soit encore: .
En posant , la dernière relation s'écrit .
Cela implique que g est bel et bien constante, donc ou bien .
Il ne reste maintenant que de remplacer dans l'équation initiale; seule a=0 convient.
L'équation fonctionnelle proposée admet une et une seule solution qui est l'identité sur .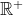
Sauf ereurs.

.

nmo , je vous prie de bien lire ce que j'avais fais
la relation g(x+y)=g(x)+g(y) est vrai
pour tout x >= a^4 et y>=0
il suffit de remplacer x-> x+a^4 avec x >=0

nmo a écrit:

On a .
On pose , l'équation fonctionnelle devient: .
Soit encore: .
En posant , la dernière relation s'écrit .
Cela implique que g est bel et bien constante, donc

c'est faux comment tu peux affirmer que tout x dans R+ peut s'ecrire xf(x)+f(x)²+z ?

Oty a écrit:

nmo , je vous prie de bien lire ce que j'avais fais
la relation g(x+y)=g(x)+g(y) est vrai
pour tout x >= a^4 et y>=0
il suffit de remplacer x-> x+a^4 avec x >=0

Pour dire que et , tu as considéré que .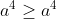
La solution est maintenat claire pour moi. Merci.

Oty a écrit:

nmo a écrit:

On a .
On pose , l'équation fonctionnelle devient: .
Soit encore: .
En posant , la dernière relation s'écrit .
Cela implique que g est bel et bien constante, donc

c'est faux comment tu peux affirmer que tout x dans R+ peut s'ecrire xf(x)+f(x)²+z ?

Peut tu bIen préciser la faute Othmane !!!!

alidos a écrit:

Peut tu bIen préciser la faute Othmane !!!!

pour le passage de g(quelquechose )=quelquechose a g(x)=x quelque soit x
il faut d'abord etre sur que tout ''x'' peut s'ecrire sous la forme de ce ''quelquechose''
par exemple considérant que dans une equation ou l'ensemble est de définition et d'arrivé de la fonction est R
est on est arrivé a un stade ou on a montrer que :
g(x²+1)=x²+1
ce le ne permet pas de déduire directement g(y)=y quelque soit y ceci est vrai que pour les reél >= 1 , c'est le meme principe .

nmo a écrit:

La solution est maintenat claire pour moi. Merci.

AU Plaisir Cher nmo

Oty a écrit:

c'est le cas ou g est Minoré et Monotone (par injectivité de f ) de l'equation de Cauchy , tu peux faire des recherches ...

mais , comment tu as démontrer que f est monotone