| | exercice de limite de ln(x) |  |
|
|
| Auteur | Message |
|---|
moulim
Maître
 Nombre de messages : 120 Nombre de messages : 120
Age : 29
Date d'inscription : 14/11/2012
 |  Sujet: exercice de limite de ln(x) Sujet: exercice de limite de ln(x)  Lun 03 Déc 2012, 13:57 Lun 03 Déc 2012, 13:57 | |
| 1) (quelque soit a dans l'ensemble R)
montrer que ; lim xln(1+a/x)=a lorsque x tend vers (+l'infini)
2) (a et b deux élèment dans l'ensemble R)
calculer ; lim ax-lnx/bx+lnx lorsque x tend vers (+l'infini)
et merci | |
|
  | |
haiki55
Maître
 Nombre de messages : 121 Nombre de messages : 121
Age : 34
Date d'inscription : 22/09/2010
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 14:45 Lun 03 Déc 2012, 14:45 | |
| Bonjour ,
Indications:
1) Effectuer le changement de variable h=a/x pour se ramener à la limite classique lim( ln(1+h)) /h lorsque h tend vers 0 .
2)Ecrire le numérateur (ax-lnx) sous la forme x.(a-(lnx)/x) et le dénominateur bx+lnx sous la forme x.(b+(lnx)/x) puis conclure en utilisant la limite classique lim (lnx)/x lorsque x tens vers +l'infini.
Remarque: Pour 2) , j'ai supposé qu'il s'agit de lim(ax-lnx)/(bx+lnx) lorsque x tens vers +l'infini. Si ce n'est pas le cas , je t'invite à réécrire l'énoncé de manière correcte en utilisant les parenthèses. | |
|
  | |
moulim
Maître
 Nombre de messages : 120 Nombre de messages : 120
Age : 29
Date d'inscription : 14/11/2012
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 17:05 Lun 03 Déc 2012, 17:05 | |
| 1) je comprends mais lim(ln(1+h))/h lorsque h tend vers 0 égale 1 non a
| |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 18:00 Lun 03 Déc 2012, 18:00 | |
| Mr Moulim Pourquoi tu Postes tes exercices ghir comme ça . faut savoir B3da de quoi il s'agit . | |
|
  | |
moulim
Maître
 Nombre de messages : 120 Nombre de messages : 120
Age : 29
Date d'inscription : 14/11/2012
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 18:33 Lun 03 Déc 2012, 18:33 | |
| merci le prof alidos
est ce que tu m'aide ?
explique moi s'il vous plait
pourquoi lim(ln(1+h))/h lorsque h tend vers 0 égale 1 non a | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 18:41 Lun 03 Déc 2012, 18:41 | |
| Lemme : }{x}=%20\alpha) Pour tout 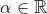 | |
|
  | |
haiki55
Maître
 Nombre de messages : 121 Nombre de messages : 121
Age : 34
Date d'inscription : 22/09/2010
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 19:52 Lun 03 Déc 2012, 19:52 | |
| Bonsoir ,
@moulim
Pour la question 1) , je t'ai donné une indication . A toi de faire le reste du travail : exprimer x.ln(1+a/x) en fonction de la nouvelle variable h (qui tend vers 0 lorsque x tend vers +l'infini) puis calculer la limite de l'expression obtenue lorsque h tend vers 0.
Un conseil:Travaillez,travaillez et encore travaillez. C'est le seul moyen pour progresser et c'est la seule chose qui vous sera utile le jour de l'examen.
Amicalement. | |
|
  | |
Tog
Féru

 Nombre de messages : 47 Nombre de messages : 47
Age : 38
Date d'inscription : 28/11/2012
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Lun 03 Déc 2012, 22:30 Lun 03 Déc 2012, 22:30 | |
| Juste remarquer que ln(1+ax) / x = [ln(1+ax)-ln(1+a*0)] / [x-0] = [f(x)-f(0)] / [x-0] avec f(x)=ln(1+ax) et donc la limite en 0 est égale à f ' (0)=a (définition du nombre dérivé) | |
|
  | |
moulim
Maître
 Nombre de messages : 120 Nombre de messages : 120
Age : 29
Date d'inscription : 14/11/2012
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  Mar 04 Déc 2012, 11:29 Mar 04 Déc 2012, 11:29 | |
| merci mr tog et mr alidos et mr haiki55
je comprends | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exercice de limite de ln(x) Sujet: Re: exercice de limite de ln(x)  | |
| |
|
  | |
| | exercice de limite de ln(x) |  |
|
