|
| | Jolie!!! |  |
| | | Auteur | Message |
|---|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Jolie!!! Sujet: Jolie!!!  Mar 12 Mar 2013, 19:50 Mar 12 Mar 2013, 19:50 | |
| a,b,c des nombres positives tel que abc=1 montrer que: 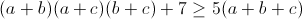 | |
|   | | bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Jeu 09 Jan 2014, 19:38 Jeu 09 Jan 2014, 19:38 | |
| Peux tu poster la reponse stp !!? | |
|   | | elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 62
Localisation : Maroc.
Date d'inscription : 24/01/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Ven 02 Avr 2021, 19:14 Ven 02 Avr 2021, 19:14 | |
| Bonjour , Sous les hypothèses : a , b , c > 0 et abc = 1 , si on note : u = u(a,b,c) = a + b + c et v = v(a,b,c) = ab + bc + ca = 1/a + 1/b + 1/c , l'inégalité demandée s'écrit : (u-a)(u-b)(u-c) +7 >= 5u , soit après développement : uv + 6 >= 5u , ou encore : v + 6/u >= 5on distingue alors deux cas :  si v >= u , alors : v + 6/u >= u + 6/u et comme , u + 6/u - 5 = (u² -5u + 6)/u = (u-3)(u-2)/u >= 0 car u >= 3 , d'après l'inégalité arithmético-géométrique : (a+b+c)/3 >= (abc)^(1/3) = 1 , on voit que dans ce cas l'inégalité demandée est satisfaite avec égalité si et seulement si a = b = c = 1 | |
|   | | elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 62
Localisation : Maroc.
Date d'inscription : 24/01/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Ven 02 Avr 2021, 19:21 Ven 02 Avr 2021, 19:21 | |
|  si u <= v , alors : on applique le cas précédent au triplet (1/a , 1/b , 1/c) (qui vérifie les mêmes hypothèses) vu que u(1/a,1/b,1/c) = v(a,b,c) et v(1/a,1/b,1/c) = u(a,b,c)  sauf erreur de ma part bien entendu sauf erreur de ma part bien entendu | |
|   | | elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 62
Localisation : Maroc.
Date d'inscription : 24/01/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Ven 02 Avr 2021, 20:26 Ven 02 Avr 2021, 20:26 | |
| Pardon (erreur de frappe)  , le second cas est plutôt :  si u >= v , alors ...  | |
|   | | naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: .. Sujet: ..  Lun 05 Avr 2021, 07:41 Lun 05 Avr 2021, 07:41 | |
| - elhor_abdelali a écrit:
 si u <= v , alors : si u <= v , alors :
on applique le cas précédent au triplet (1/a , 1/b , 1/c) (qui vérifie les mêmes hypothèses)
vu que u(1/a,1/b,1/c) = v(a,b,c) et v(1/a,1/b,1/c) = u(a,b,c)  sauf erreur de ma part bien entendu sauf erreur de ma part bien entendu Si v'(1/a,1/b,1/c) => u'(1/a,1/b,1/c) alors v'+6/u' >= 5, soit (1/b +1/c)(1/c +1/a)(1/a +1/b) +7 >= 5(1/a +1/b +1/c). | |
|   | | elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 62
Localisation : Maroc.
Date d'inscription : 24/01/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Lun 05 Avr 2021, 19:28 Lun 05 Avr 2021, 19:28 | |
| Oui nail tu as parfaitement raison je réfléchis encore au cas u >= v  | |
|   | | naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Mar 06 Avr 2021, 08:42 Mar 06 Avr 2021, 08:42 | |
| Si r=(a+b)u, s=(b+c)u, t=(c+a)u étaient en unité u de longueur les côtés d'un triangle, alors 2p=2(a+b+c)u=r+s+t serait son périmètre, S=√{p(p-r)(p-s)(p-t)} serait son aire, et l'inégalité serait formulée rst+7u³>=5pu², or S=√{pu³} traduit la contrainte abc=1. Mais S=rst/{4R}, où R représente le rayon du cercle circonscrit au triangle, tel que 2R = r /sin x = s /sin y = t /sin z, comme relations de sinus dans le triangle. Aussi,
2R = 2p /{sin x + sin y + sin z} dont le minimum à périmètre égal est atteint pour x=y=z=π/3, donc l'inégalité pourrait se réduire au cas particulier 8p√{3pu} /9 +7u² >= 5pu, ou encore 8√3 /9 *P³ +7 >= 5P² où la variable adimensionnée P=√{a+b+c} est telle que P² >=3 *³√{abc} = 3. | |
|   | | naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Mer 07 Avr 2021, 13:36 Mer 07 Avr 2021, 13:36 | |
| - naïl a écrit:
- (..)
2R = 2p /{sin x + sin y + sin z} dont le minimum à périmètre égal est atteint pour (..) Cette simplification est pas suffisante, outre que le triangle équilatéral n'est pas valable pour toutes valeurs de p à cause de la condition abc=1. | |
|   | | elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 62
Localisation : Maroc.
Date d'inscription : 24/01/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Lun 19 Avr 2021, 01:42 Lun 19 Avr 2021, 01:42 | |
| Bonsoir ,
https://www.ilemaths.net/sujet-une-inegalite-866579.html | |
|   | | naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Ven 07 Mai 2021, 11:36 Ven 07 Mai 2021, 11:36 | |
| Les sommes b+c, c+a et a+b pourraient être les longueurs des côtés d'un triangle XYZ en unités de longueur u. Si R est le rayon de son cercle circonscrit, p la demi-longueur de son périmètre, et x, y et z les mesures en radians respectives de ses angles intérieurs en ses sommets X, Y et Z, alors l'inégalité équivaut à
4Ru^-1 √{pu^-1} +7 >= 5pu^-1 tel que
R=½(sin x sin y sin z sin{x/2} sin{y/2} sin{z/2})^{-1/3} u et p=(tan{x/2} tan{y/2} tan{z/2})^{-2/3} u; ce quels que soient x, y et z tels q x+y+z=π, car la condition abc=1 est réalisable pour tout triangle XYZ par homothétie.
| |
|   | | naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Lun 24 Mai 2021, 15:49 Lun 24 Mai 2021, 15:49 | |
| L'inégalité est équivalente à ce que la fonction 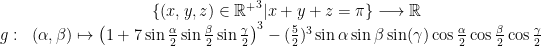 soit positive.(il manque la variable gamma comme troisième attribut) | |
|   | | naïl
Maître

 Nombre de messages : 221 Nombre de messages : 221
Age : 42
Date d'inscription : 25/04/2006
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  Lun 24 Mai 2021, 18:53 Lun 24 Mai 2021, 18:53 | |
| Dans les inégalités des moyennes MH <= MG <= MA, où MH=3/v, MG=1 et MA=u/3 dans ce cas. En plus, si a, b et c sont différents, alors MH < MG < MA, et pour tout alpha nombre réel positif inférieur à 1, {1 /MA < alpha /MH +{1 -alpha} /MA < 1 /MH}. Ce pour tous nombres a, b et c sans que nécessairement abc=1. Or l'exercice stipule que v +6/u >= 5, donc {3 /MH +2 /MA >= 5} si abc=1, { 3 /MH +2 /MA >= 5 /MG} pour a, b et c quelconques positifs( les nombres a/³√{abc}, b/³√{abc} et c/³√{abc} ont des moyennes harmonique et arithmétique égales aux moyennes harmonique et arithmétique des nombres a, b et c divisées par leur moyenne géométrique ³√{abc} respectivement). | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Jolie!!! Sujet: Re: Jolie!!!  | |
| |
|   | | | | Jolie!!! |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
