EXO difficile

Soit n un entier naturel non nul
Prouver que : 1+1/2^2+1/3^2+...+1/n^2<ou=1

C'est plus petit que 2 pas 1

Merci ! Tbarkellah 3lik (meme si f l enonce j ai <=1)
J'ajoute un autre Calculez
A=[n/n(n+1)]+[n/(n+1)(n+2)]+.....+[2n/(2n)(2n+1)]

Il suffit de remarquer que


-
-
-

alors après une simplification on onra

Je ne comprends pas un Truc:
Pourquoi

Et Pas: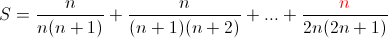

Je parle du 2n dans le dernier Terme

OUI C'est ça ce qu’on doit avoir

Dsl dsl j suis vraiment desole y a une faute dans l enonce
la derniere c est n/2n(2n+1)
Dsl dsl j suis vraiment desole ...

En effet le resultat juste doit etre

1-n/2n+1
Sauf erreur

Oui c'est la bonne réponse (de la même méthode qu'a fait L-W-P, juste en rectifiant la faute d'énoncé)