fonction convexe ?

j'ai un petit qestion qui me confuse sur les fonctions , quelle est la définition d'une fonction convexe ?   
et si vous voulez me donner des exemples pr bien comprendre et merci   

Bon voila la definition, et son interpretation geo
Soient I un intervale et f:I:->R une fonction numérique. LA fonction f est dite convexe sur I si pour tous x_1 et x_2 dans I, on a:
pour toute \lambda de [0;1]
Geomètriquement on dit que f est convexe si pour touts x, y de I le segment le segment [XY] est en haut de la représentation de f, où X(x;f(x)) et Y(y;f(y)). ( de cette interpretation geometrique on peut sortir la definition)

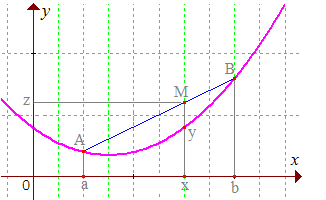
Encore une autre manière, si f est deux fois dérivable sur I, alors f convexe <==> f''>0 . En d'autre terme la pente de f est croissante ( ou bien lmayl dial les tangantes à la courbe augmentent ) voici une image qui illustre cela .

Finalement f concave si -f convexe.
Hope you liked it. Et j'espère ne pas avoir fait d'erreur.