| | saisir les théorémes |  |
|
+3Ahmed Taha legend-crush L-W-P 7 participants |
|
| Auteur | Message |
|---|
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: saisir les théorémes Sujet: saisir les théorémes  Mer 05 Fév 2014, 12:34 Mer 05 Fév 2014, 12:34 | |
| A fin de bien saisir les théorèmes et bien les manipuler je propose de lancer un sujet consacré aux TH est ses applications.
On va traiter les théorèmes une par une.Chacune va prendre au maximum 3 jours.
pour commencer je préfère celle de l'inégalité triangulaire
comme EXO 1
montrer pour tous réels a,b
llal-lbll=<la-bl=<lal+lbl (c'est facile)
celui qui répond qu'il poste un exercice de l'inégalité triangulaire. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 12:49 Mer 05 Fév 2014, 12:49 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 12:51 Mer 05 Fév 2014, 12:51 | |
| Exo 2: (C'est aussi facile) Montrer que: 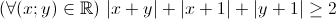 Determinez le cas d'égalité | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 13:15 Mer 05 Fév 2014, 13:15 | |
| REPONSE EXO 2
le fait c'est de constater ( a partir de exercice 1) que lal+lbl>=la-bl
alors lx+yl+lx+1l+ly+1l>=l1-yl+ly+1l>=2
| |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 18:43 Mer 05 Fév 2014, 18:43 | |
| cas d'égalité lorsque (x=1 et y=-1) ou (x=-1 et y=1) | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 18:57 Mer 05 Fév 2014, 18:57 | |
| EXO 3
soient a.b.c les longueurs d'un triangle tels que a^2+b^2>5c^2
prouver que c est la plus petite longueur de ce triangle. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 19:27 Mer 05 Fév 2014, 19:27 | |
| - S 3:
b<a+c et a^2+b^2>5c^2 donc 2a^2+c^2+2ac>5c^2 => a^2+ac>2c^2 => (a-c)(a+2c)>0 => a>c
la même chose pour démontrer que b>c
alors c est la plus petite longueur de ce triangle.
- P 4:
a,b,c les mesures des cotés d'un triangle tel que a<b<c
montrez que (a+b+c)^2>4(a^2+b^2).
Dernière édition par Ahmed Taha le Jeu 06 Fév 2014, 00:19, édité 3 fois | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 05 Fév 2014, 19:37 Mer 05 Fév 2014, 19:37 | |
| c'est ça.A toi de poster un exo d'inégalité triangulaire. | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 05:50 Jeu 06 Fév 2014, 05:50 | |
| Réponse exo 4
(c>a)----(2ac>2a^2) et (c>b)-----(2bc>2b^2)et(c^>b^2)et(b>a)---(2ab>a^2)
en sommant on va avoir
c^2+2ac+2ab+2bc>3a^2+3b^2
ce qui donne
(a+b+c)^2>4(a^2+b^2)
Dernière édition par L-W-P le Ven 07 Fév 2014, 07:25, édité 1 fois | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 12:43 Jeu 06 Fév 2014, 12:43 | |
| exo 5
x,y des réels monter que
http://latex.codecogs.com/gif.latex?%5Cfrac%7B%5Cleft%20%7C%20x+y%20%5Cright%20%7C%7D%7B1+%5Cleft%20%7C%20x+y%20%5Cright%20%7C%7D%5Cleq%20%5Cfrac%7B%5Cleft%20%7Cx%20%5Cright%20%7C%7D%7B1+%5Cleft%20%7C%20x%20%5Cright%20%7C%7D+%5Cfrac%7B%5Cleft%20%7C%20y%20%5Cright%20%7C%7D%7B1+%5Cleft%20%7Cy%20%5Cright%20%7C%7D | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 13:40 Jeu 06 Fév 2014, 13:40 | |
| - L-W-P a écrit:
- Réponse exo 4
(c>a)----(2ac>2a^2) et (c>b)-----(2ac>2b^2)et(c^>b^2)et(b>a)---(2ab>a^2)
en sommant on va avoir
c^2+2ac+2ab+2bc>3a^2+3b^2
ce qui donne
(a+b+c)^2>4(a^2+b^2) Pourquoi 2ac> 2b^2 ?? | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 16:31 Jeu 06 Fév 2014, 16:31 | |
| - L-W-P a écrit:
- exo 5
x,y des réels monter que
 - S 5:
pr tt a,b >0 si a >b alors 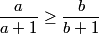 on a |x|+|y|+|xy| >|x+y| donc 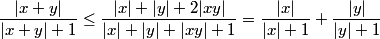
| |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 20:02 Jeu 06 Fév 2014, 20:02 | |
| - Ahmed Taha a écrit:
- L-W-P a écrit:
- Réponse exo 4
(c>a)----(2ac>2a^2) et (c>b)-----(2ac>2b^2)et(c^>b^2)et(b>a)---(2ab>a^2)
en sommant on va avoir
c^2+2ac+2ab+2bc>3a^2+3b^2
ce qui donne
(a+b+c)^2>4(a^2+b^2) Pourquoi 2ac> 2b^2 ?? c'est 2bc>2b^2 PS: faute de frappe | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 20:04 Jeu 06 Fév 2014, 20:04 | |
| quelqu'un poste un exo dans l'inégalité triangulaire.
| |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 06 Fév 2014, 22:44 Jeu 06 Fév 2014, 22:44 | |
| - P 6:
Soient a,b et c trois réels tels que : |ab−c|= 3. Trouver la plus petite valeur de l'expression a²+b²+c².
| |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Ven 07 Fév 2014, 21:40 Ven 07 Fév 2014, 21:40 | |
| j'ai procedé ainsi
lab-cl = 3 <==> (ab)² + c² = 3 + 2abc > 0 ==> abc >= -3/2
On applique I.A.G : (a²+b²+c²) >= (3v)a²b²c² >= 3v(9/4) (3v) = racine troisiéme
mais je pense que abc doit etre positive :/
sinon quand abc < 0 j'ai trouvé que la plus petite valeure est 9 | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Dim 09 Fév 2014, 00:03 Dim 09 Fév 2014, 00:03 | |
| M. Ahmed TAHA a proposé l'exercice suivant:
Soient a,b et c trois réels tels que : |ab−c|= 3. Trouver la plus petite valeur de l'expression a²+b²+c².
Voici une tentative de résolution de cet exercice:
|ab-c| = 3 <--> (ab-c = 3 ou ab-c = -3) <--> (c=ab-3 ou c=ab+3)
<--> c^2 = a^2 b^2 + 9 - 6 ab ou c^2 = a^2 b^2 + 9 + 6 ab,
donc a^2 + b^2 + c^2 = a^2 + b^2 + a^2 b^2 + 9 - 6 ab ou a^2 + b^2 + c^2 = a^2 + b^2 + a^2 b^2 + 9 + 6 ab .
Comme a^2 + b^2 + a^2 b^2 + 9 > 0 , donc dans le contexte de la recherche de la valeur minimale de a^2 + b^2 + c^2, on doit opter pour une valeur de (6 ab) ou (-6 ab) qui minimise a^2 + b^2 + c^2, donc on doit avoir (6 ab = - 6 |a| |b| ou - 6 ab = - 6 |a| |b|), donc dans les deux cas on a:
a^2 + b^2 + c^2 = a^2 + b^2 + a^2 b^2 + 9 - 6 |a||b| = (|a|-|b|)^2 + (|a||b| - 2)^2 + 5, expression qui est minimale quand elle est égale à 5, mais à condition que le système (|a|-|b|=0 et |a||b| - 2 = 0) soit solvable.
On a |a|-|b|= 0 et |a||b| - 2 = 0 <--> |a|= |b| et |a||b| = a^2 = 2 <--> |a|= |b| et |a| = 2^(1/2), donc le système est solvable, et par conséquent la valeur minimale de a^2 + b^2 + c^2 quand |ab−c|= 3 est 5.
Cette démonstration - si elle exempte d'erreurs - est très longue, et je suis sûr que M. Ahmed TAHA a une solution très élégante à nous proposer.
A propos, je le félicite pour la merveilleuse démonstration de l'exercice 5: l'astuce utilisé m'a permis de résoudre plusieurs exercices qui me tracassaient. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Dim 09 Fév 2014, 07:49 Dim 09 Fév 2014, 07:49 | |
| En relisant ma démonstration, j'ai trouvé qu' il était préférable d' y introduire quelques modifications comme suit:
|ab-c| = 3 <--> (ab-c = 3 ou ab-c = -3) <--> (c=ab-3 ou c=ab+3)
<--> c^2 = a^2 b^2 + 9 - 6 ab ou c^2 = a^2 b^2 + 9 + 6 ab,
donc a^2 + b^2 + c^2 = a^2 + b^2 + a^2 b^2 + 9 - 6 ab ou a^2 + b^2 + c^2 = a^2 + b^2 + a^2 b^2 + 9 + 6 ab
<--> a^2 + b^2 + c^2 = (a^2 + b^2 - 2 ab) + (a^2 b^2 + 4 - 4 ab) + 5 ou a^2 + b^2 + c^2 = (a^2 + b^2 + 2 ab) + (a^2 b^2 + 4 + 4 ab) + 5
<--> a^2 + b^2 + c^2 = (a - b)^2 + (ab - 2)^2 + 5 ou a^2 + b^2 + c^2 = (a + b)^2 + (ab + 2)^2 + 5
donc dans les deux cas, la valeur minimale de a^2 + b^2 + c^2 quand |ab−c|= 3 est 5.
On peut généraliser cette méthode pour k >= 1/2 qui donne que la valeur minimale de a^2 + b^2 + c^2 quand |ab−c|= k est (2k - 1).
Pour k = 0, on a (ab = c) et la valeur minimale de a^2 + b^2 + c^2 quand |ab−c|= 0 est 0.
J’espère que c'est juste. | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Lun 10 Fév 2014, 12:24 Lun 10 Fév 2014, 12:24 | |
| Passant maintenant à une deuxième théorème celle de HÖLDER (Cauchy Schwartz)
comme exo 1
k et n sont de N , montrer que
http://latex.codecogs.com/gif.latex?%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cfrac%7B1%7D%7Bk_%7Bi%7D%5E%7B2%7D%7D%5Cgeq%20%5Cfrac%7B6n%7D%7B%28n+1%29%282n+1%29%7D
celui qui répond qu'il poste un exercice dans cette théorème.
Dernière édition par L-W-P le Lun 10 Fév 2014, 16:59, édité 1 fois | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Lun 10 Fév 2014, 16:16 Lun 10 Fév 2014, 16:16 | |
| Permettez-moi de penser qu' il s'agit de "sigma 1/k^2" et non de "sigma 1/k". | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Lun 10 Fév 2014, 16:57 Lun 10 Fév 2014, 16:57 | |
| oui c'est ça pardon pour cette faute. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Lun 10 Fév 2014, 17:11 Lun 10 Fév 2014, 17:11 | |
| | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Lun 10 Fév 2014, 17:22 Lun 10 Fév 2014, 17:22 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 | |
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  | |
| |
|
  | |
| | saisir les théorémes |  |
|
