| | saisir les théorémes |  |
|
+3Ahmed Taha legend-crush L-W-P 7 participants |
|
| Auteur | Message |
|---|
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 | |
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Mer 12 Fév 2014, 15:27 Mer 12 Fév 2014, 15:27 | |
| - aymanemaysae a écrit:
- M. L-W-P m'a conseillé de poster cet exercice ici: je l'avais posté par erreur dans un autre contexte.
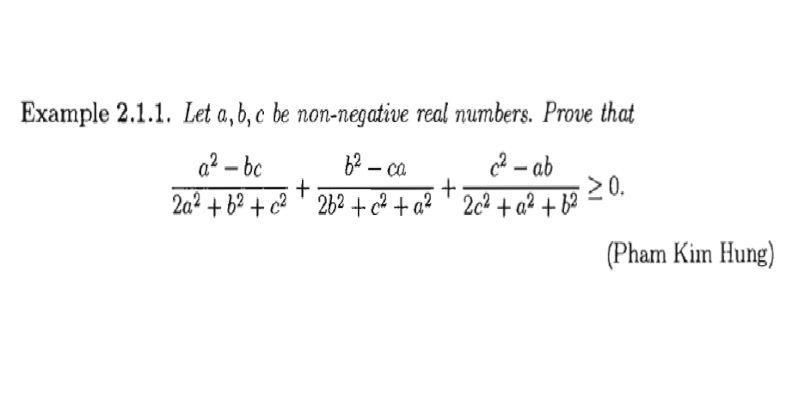 voici ma solution l'inégalité est homogène  cette fois Je n'ai pas trouvé une bon méthode | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 12:48 Jeu 13 Fév 2014, 12:48 | |
| Un Maître reste toujours un Maître. Votre solution est un cours riche d'astuces et d'un niveau technique élevé: je ne peux qu'en vous remercier. La solution que je propose et que j'ai trouvée dans la même page que l'exercice en question,est certes succincte mais n'est pas très instructive:  Merci. | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 18:56 Jeu 13 Fév 2014, 18:56 | |
| Je ne comprends pas le passage où on a appliqué Caushy Shwartz | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 19:15 Jeu 13 Fév 2014, 19:15 | |
| - aymanemaysae a écrit:
- Un Maître reste toujours un Maître. Votre solution est un cours riche d'astuces et d'un niveau technique élevé: je ne peux qu'en vous remercier.
La solution que je propose et que j'ai trouvée dans la même page que l'exercice en question,est certes succincte mais n'est pas très instructive:

Merci. Merci bcp Mr aymanemaysae c une bonne solution - Sketshup a écrit:
- Je ne comprends pas le passage où on a appliqué Caushy Shwartz
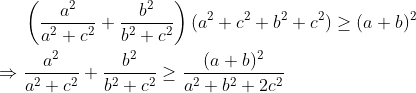 il y a une autre généralisation de Holder 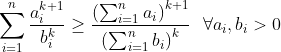 prend n=2,k=1,a_1=a,a_2=b,b_1=a²+c² et b_2=b²+c² ... | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 20:12 Jeu 13 Fév 2014, 20:12 | |
| | |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 20:37 Jeu 13 Fév 2014, 20:37 | |
| Pose un nouveau exo , merci | |
|
  | |
Lonely.Guy
Débutant

 Nombre de messages : 8 Nombre de messages : 8
Age : 27
Date d'inscription : 13/02/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 21:16 Jeu 13 Fév 2014, 21:16 | |
| MQ Pour tout a,b et c £ (R*+)^3  | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 21:32 Jeu 13 Fév 2014, 21:32 | |
| Multiplier les 3 termes par le même dénominateur, produis en croix, simplifier.
On en vient à (SOMME Sym) a²b >= 6abc, qui est une application directe de AM-GM.
Peu élégante, mais cette méthode d'attaque m'a parut plus simple.
Mon post:
Je prends le droit de changer un peu des inégalités. Place à un peu d'arithmétique!
Résoudre l'équations diophantienne suivante (échauffement nocturne):
a^3 + 2b^3 = 4c^3 | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 22:08 Jeu 13 Fév 2014, 22:08 | |
| En réponse à l'exercice de M. Lonely Guy, je propose la solution suivante: si elle est juste, je proposerai un exercice pour saisir un théorème que je vous laisse l'honneur de choisir:  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 22:41 Jeu 13 Fév 2014, 22:41 | |
| - Sketshup a écrit:
Mon post:
Résoudre l'équations diophantienne suivante (échauffement nocturne):
a^3 + 2b^3 = 4c^3 La seule solution est (0.0.0) ??! (descente infinie) | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Jeu 13 Fév 2014, 23:36 Jeu 13 Fév 2014, 23:36 | |
| - Lonely.Guy a écrit:
- MQ
Pour tout a,b et c £ (R*+)^3  voici une autre solution : selon Caushy 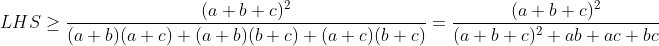 on a 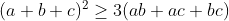 alors 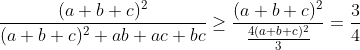 | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Ven 14 Fév 2014, 00:00 Ven 14 Fév 2014, 00:00 | |
| - Sketshup a écrit:
- Résoudre l'équations diophantienne suivante (échauffement nocturne):
a^3 + 2b^3 = 4c^3 si d=pgcd(a,b) alors d|c et le même résultat pour les autre donc pgcd(a,b)=pgcd(a,c)=pgcd(b,c)=pgcd(a,b,c)=d pour d=0 on trouve S={(0,0,0)} pour d=/=0 posons a=dx,b=dy et c=dz avec pgcd(x,y)=pgcd(x,z)=pgcd(y,z)=1 on a x^3+2y^3=4z^3 alors x^3=2(2z^3-y^3) donc 2|x^3 => 2|x (*) => il existe k / x=2k alors 4k^3=2z^3-y^3 => y^3=2(z^3-2k^3)=>2|x^3 => 2|y (**) après les deux relations on trouve que pgcd(x,y)=/=1 contradiction alors (0,0,0) est la seul solution. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Ven 14 Fév 2014, 10:17 Ven 14 Fév 2014, 10:17 | |
| Une autre solution qui utilise le principe de la descente infinie,est comme suit:
Cas n° 1: Soient a,b et c des entiers naturels non nuls.
a^3 + 2 b^3 = 4 c^3 induit que a = 2 A (A entier naturel tel que A < a),
donc 8 A^3 + 2 b^3 = 4 c^3, donc 4 A^3 + b^3 = 2 c^3 qui induit que b = 2 B (B entier naturel tel que B < b),
donc 4 A^3 + 8 B^3 = 2 c^3, donc 2 A^3 + 4 B^3 = c^3 qui induit aussi que c = 2 C (C entier naturel tel que C < c),
donc 2 A^3 + 4 B^3 = 8 C^3, donc A^3 + 2 B^3 = 4 C^3 : équation de la même forme que a^3 + 2 b^3 = 4 c^3
avec A < a, B < b et C < c, donc par le principe de la descente infinie, cette équation n'admet pas de solution
tel que (a;b;c) un triplet de IN* x IN* x IN* .
Cas n° 2: Soient a, b et c des entiers naturels dont au moins un est nul (abc = 0).
L'équation s'écrit donc sous l'une des formes suivantes: b^3 = 2 c^3 ou a^3 = 4 c^3 ou
a^3 + 2 b^3 = 0, ce qui donne toujours une solution triviale (a;b;c) = (0;0;0) . | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  Ven 14 Fév 2014, 12:04 Ven 14 Fév 2014, 12:04 | |
| Pour ne pas rester passif, voici un petit exercice qui est un cas particulier d'un cas plus général:
c'est un exercice que j'appelle "Le Colosse aux pieds d'argile" car il contient de grands
nombres, mais dont l'astuce pour le résoudre est simple.
Montrer que 10001^10001 + 10001^401 peut s'écrire sous la forme
de deux carrés parfaits. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: saisir les théorémes Sujet: Re: saisir les théorémes  | |
| |
|
  | |
| | saisir les théorémes |  |
|
