|
| | Révision mais pour les 1er bac |  |
| | |
| Auteur | Message |
|---|
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Révision mais pour les 1er bac Sujet: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:12 Sam 22 Mar 2014, 19:12 | |
| Puisque cette année constitue un tournant dans les mathématiques et ainsi qu'on est intéressé par les concours scientifiques, je lance ce sujet pour réviser tous les leçons du programme. Évidement la logique est la première leçon. Or tout le programme est de la logique. Commençant par la leçon 1 les ensembles .La durée de cette leçon est 3 jours, après on passe à une autre. j’espère que tous les 1er bac participent, et que nos ancêtres nous renseignent par des astuces et des aides. Mais rapidement. comme EXO 1A=4n^2+4n-47 1) montrer que A est impair. 2) soit A un carré parfait 1-montrer que il existe un k de IN tels que A=(2k+1)^2 2-déduire que (n-k)(n+k+1)=12 3)  Déterminer 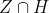 rapidement celui qu'il répond qu'il poste, même un exo facile. P.S:Réponse complète.
Dernière édition par L-W-P le Sam 22 Mar 2014, 19:43, édité 1 fois | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:25 Sam 22 Mar 2014, 19:25 | |
| emm trés bonne idée j'ai honneur de participe avc vous inch2allah ^^ | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:27 Sam 22 Mar 2014, 19:27 | |
| merci pour ta réponse tu m'as passionné. | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:38 Sam 22 Mar 2014, 19:38 | |
| A est impair mr LWP tu peux l'éditer  | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:43 Sam 22 Mar 2014, 19:43 | |
| | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:46 Sam 22 Mar 2014, 19:46 | |
| 1) On a +1) donc 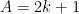 avc 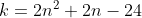 2)Montrons que A est un carré parfait : On a ^{2}-48) (2n+1+4\sqrt{3}%20)) (2k%27+1)) 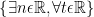 tel que 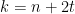 (variable) avc 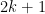 carré parfait ! donc A=(2k+1)^2 | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 19:53 Sam 22 Mar 2014, 19:53 | |
| pour le 2
c'est juste une déduction de 1
A=2p+1 et A=q^2 (k et q de Z°
alors q^2=2p+1 d'où q=2k+1
et encore A=(2k+1)^2
Mais l'essentiel c'est le 3 | |
|   | | legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 | |   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 | |   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:18 Sam 22 Mar 2014, 20:18 | |
| indice
calculer le discriminant de l'équation
2x^2x(5-2y)+x(9-2y)=0
et puis trouver la relation entre le Delta et les premières question.
Dernière édition par L-W-P le Sam 22 Mar 2014, 20:53, édité 2 fois | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:19 Sam 22 Mar 2014, 20:19 | |
| - Amiral a écrit:
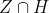 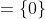 c ma solution est vraie je poste le ... c ma solution est vraie je poste le ... Solution fausse malheureusement contre exemple x=0 9/3=3 de Z | |
|   | | aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:24 Sam 22 Mar 2014, 20:24 | |
| Exo 1:
1) A=4n^2+4n-47=4n^2+4n-48+1=2(2n^2+2n-24)+1, donc A est impair.
2) 1- Comme A est impair , et comme c'est un carré parfait, donc c'est le carré d'un nombre impair, donc il existe un k de IN tels que A=(2k+1)^2 .
2- on a A=4n^2+4n-47=(2k+1)^2=4k^2+4k+1 <-->4(n^2-k^2)+4(n-k)=48 <--> n^2-k^2 + n-k = 12 <--> (n-k)(n+k)+n-k=12 <--> (n-k)(n+k+1)=12 .
3) On a (2x^2+5x+9)/(2x+3)=x+1+6/(2x+3)
(2x^2+5x+9)/(2x+3) est entier relatif <--> 2x+3 est un diviseur de 6 càd -6, -3, -2, -1, 1, 2, 3, 6 donc x= -9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2, donc
H (inter) Z = {-9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2} . | |
|   | | aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:31 Sam 22 Mar 2014, 20:31 | |
| Après votre permission M. L_W_P, si ma réponse est juste, je vous demande que vous laissiez M. Amiral poster son exercice: j'ai vu qu'il avait un exercice et qu'il allait le poster si sa solution était juste. | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:34 Sam 22 Mar 2014, 20:34 | |
| - aymanemaysae a écrit:
- Exo 1:
1) A=4n^2+4n-47=4n^2+4n-48+1=2(2n^2+2n-24)+1, donc A est impair.
2) 1- Comme A est impair , et comme c'est un carré parfait, donc c'est le carré d'un nombre impair, donc il existe un k de IN tels que A=(2k+1)^2 .
2- on a A=4n^2+4n-47=(2k+1)^2=4k^2+4k+1 <-->4(n^2-k^2)+4(n-k)=48 <--> n^2-k^2 + n-k = 12 <--> (n-k)(n+k)+n-k=12 <--> (n-k)(n+k+1)=12 .
3) On a (2x^2+5x+9)/(2x+3)=x+1+6/(2x+3)
(2x^2+5x+9)/(2x+3) est entier relatif <--> 2x+3 est un diviseur de 6 càd -6, -3, -2, -1, 1, 2, 3, 6 donc x= -9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2, donc
H (inter) Z = {-9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2} . pour la question 3 MR aymanemaysae vous a commis une erreur parceque 2x^2+5x+9)/(2x+3) est une entier<--> x et de Z et 2(x+3)l6
ce qui élimine les cas de -9/2 -5/2 -1/2 3/2
qui sont pas des solutions en remplaçant.
mais j'éspére que vous trouvez une solution en utilisant les questions précédentes
Dernière édition par L-W-P le Sam 22 Mar 2014, 20:46, édité 1 fois | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:42 Sam 22 Mar 2014, 20:42 | |
| - L-W-P a écrit:
- aymanemaysae a écrit:
- Exo 1:
1) A=4n^2+4n-47=4n^2+4n-48+1=2(2n^2+2n-24)+1, donc A est impair.
2) 1- Comme A est impair , et comme c'est un carré parfait, donc c'est le carré d'un nombre impair, donc il existe un k de IN tels que A=(2k+1)^2 .
2- on a A=4n^2+4n-47=(2k+1)^2=4k^2+4k+1 <-->4(n^2-k^2)+4(n-k)=48 <--> n^2-k^2 + n-k = 12 <--> (n-k)(n+k)+n-k=12 <--> (n-k)(n+k+1)=12 .
3) On a (2x^2+5x+9)/(2x+3)=x+1+6/(2x+3)
(2x^2+5x+9)/(2x+3) est entier relatif <--> 2x+3 est un diviseur de 6 càd -6, -3, -2, -1, 1, 2, 3, 6 donc x= -9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2, donc
H (inter) Z = {-9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2} . pour la question 3
MR aymanemaysae vous a commis une erreur parceque 2x^2+5x+9)/(2x+3) est une entier<--> x et de Z et 6l(2x+3) c (2x+3)l6
.... | |
|   | | aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:46 Sam 22 Mar 2014, 20:46 | |
| Vous avez raison M. L_W_P, lors de la résolution j'ai oublié que x devait être un entier relatif, donc:
3) On a (2x^2+5x+9)/(2x+3)=x+1+6/(2x+3)
(2x^2+5x+9)/(2x+3) est entier relatif <--> 2x+3 est un diviseur de 6 càd -6, -3, -2, -1, 1, 2, 3, 6 donc x= -3, -2, -1, 0, donc
H (inter) Z = { -3, -2, -1, 0}
Je m'excuse pour l'inadvertance, tout en insistant sur ma demande en faveur de M. Amiral.
Merci. | |
|   | | legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:48 Sam 22 Mar 2014, 20:48 | |
| J'ai trouvé une bien mauvaise méthode, où je n'ai pas eu l'occasion d'utiliser les précédantes questions. Mais bon ... je tacherai à la partager plutard vu que là, l'internet se fout carrément de ma gueule (meme codecogs ne veut pas marcher ) :'(
P.S: Mr aymane maysae, x n'est pas un entier relatif mais un rationnel
donc (2x^2+5x+9)/(2x+3) entier ne veut pas certainement dire que 6/(2x+3)
entier vu que il te reste l'autre membre x+1 qui lui n'est pas entier
Amicalement!! | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:49 Sam 22 Mar 2014, 20:49 | |
| - aymanemaysae a écrit:
- Exo 1:
1) A=4n^2+4n-47=4n^2+4n-48+1=2(2n^2+2n-24)+1, donc A est impair.
2) 1- Comme A est impair , et comme c'est un carré parfait, donc c'est le carré d'un nombre impair, donc il existe un k de IN tels que A=(2k+1)^2 .
2- on a A=4n^2+4n-47=(2k+1)^2=4k^2+4k+1 <-->4(n^2-k^2)+4(n-k)=48 <--> n^2-k^2 + n-k = 12 <--> (n-k)(n+k)+n-k=12 <--> (n-k)(n+k+1)=12 .
3) On a (2x^2+5x+9)/(2x+3)=x+1+6/(2x+3)
(2x^2+5x+9)/(2x+3) est entier relatif <--> 2x+3 est un diviseur de 6 càd -6, -3, -2, -1, 1, 2, 3, 6 donc x= -9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2, donc
H (inter) Z = {-9/2 , -3, -5/2, -2, -1, -1/2 , 0, 3/2} . lorsque on dit que l'ensemble Z inter H càd les éléments communs de Z et H en meme temps alors pr votre solution mr.aymen on dit que -9/2 £ Z et £ H ... (impossible)  on prend seulment les entiers relatifs n'est pas ??????  | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:50 Sam 22 Mar 2014, 20:50 | |
| puisque la solution en utilisant les premières questions, n'est pas encore postée je préfère de ne pas poster une exo 2
parce que arriver à l'aide de ces questions, donne un goût particulier à cet exo.
Dernière édition par L-W-P le Sam 22 Mar 2014, 20:51, édité 1 fois | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:51 Sam 22 Mar 2014, 20:51 | |
| - aymanemaysae a écrit:
- Vous avez raison M. L_W_P, lors de la résolution j'ai oublié que x devait être un entier relatif, donc:
3) On a (2x^2+5x+9)/(2x+3)=x+1+6/(2x+3)
(2x^2+5x+9)/(2x+3) est entier relatif <--> 2x+3 est un diviseur de 6 càd -6, -3, -2, -1, 1, 2, 3, 6 donc x= -3, -2, -1, 0, donc
H (inter) Z = { -3, -2, -1, 0}
Je m'excuse pour l'inadvertance, tout en insistant sur ma demande en faveur de M. Amiral.
Merci. d'abord x£ Q+ ce qui élimine -3 -2 -1 comme solutions, la seule solution est 0 je pense
Dernière édition par Amiral le Sam 22 Mar 2014, 20:57, édité 1 fois | |
|   | | L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 20:53 Sam 22 Mar 2014, 20:53 | |
| indice
calculer le discriminant de l'équation
2x^2+x(5-2y)+x(9-2y)=0
et puis trouver la relation entre le Delta et les premières question.
j'ai dèja réclamé ça c'est la clé
Dernière édition par L-W-P le Sam 22 Mar 2014, 23:30, édité 1 fois | |
|   | | aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 21:08 Sam 22 Mar 2014, 21:08 | |
| M. L_W_P, je n'arrive pas à lire l'équation : 2x^2x(5-2y)+x(9-2y)=0 | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 21:36 Sam 22 Mar 2014, 21:36 | |
| en tout cas c le dernier exo des ensembles sur elmoufid ------------------------------------------------------ puisque le temps s'écoule je poste un 2éme exo : Soient a et b £ R*² Pour Tout n posons : =\prod_{p+q\leq%20n}a^pb^q) 1)Calculer %20et%20A(3)%20,) ) 2)Monter que : =(ab)^{\frac{(n+1)(n+2)}{2}}A_n) 3) Monter que : %20A(n)=(ab)^{\frac{n^3+3n^2+2n}{6}}) --------------------------------------------------------- Ps : c facile à vous de jouer ^^ | |
|   | | aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 21:57 Sam 22 Mar 2014, 21:57 | |
| Puisqu il n' y a pas de réponse à ma remarque, j' opte pour ce raisonnement:
(2x^2+5x+9)/(2x+3) est un entier relatif, donc il existe z de Z tel que:
(2x^2+5x+9)/(2x+3) = z <--> 2x^2 + (5-2z)x + (9-3z) = 0 <--> delta= 4z^2 + 4z - 47 qui est un carré parfait ssi il existe k de Z tel que (z-k)(z+k+1)=12, donc z= 6, 3, -4, -7, donc
delta = 121 pour z=6 ou z=-7
et delta = 1 pour z= 3 ou z=-4
donc x= 0 , après rectification,suite à la remarque de M. Amira : les solutions x= -1, -2, -3 sont à rejeter.
donc H (inter) Z = {0}
Dernière édition par aymanemaysae le Sam 22 Mar 2014, 22:54, édité 1 fois | |
|   | | Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  Sam 22 Mar 2014, 22:06 Sam 22 Mar 2014, 22:06 | |
| ta méthode est vraie mais x doit etre positive (x £ Q+ selon les donnés de qes 3 ) | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Révision mais pour les 1er bac Sujet: Re: Révision mais pour les 1er bac  | |
| |
|   | | | | Révision mais pour les 1er bac |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
