derivation

On considere la fonction h d'un variable x définie par : 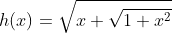$derivation Gif$

MQ : Pour tout x £ R : 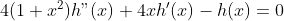$derivation Gif$

bonne chance king

Maître Nombre de messages : 238 Age : 27 Date d'inscription : 23/09/2012

solution:
il suffit de remarquer que

$derivation Gif$
$derivation Gif$
$derivation Gif$
$derivation Gif$
A=0

oui bravo c la meme méthode que j'ai fait , tu peux poster un autre exo mr LWP ? de deriv biensur ^^

Maître Nombre de messages : 238 Age : 27 Date d'inscription : 23/09/2012

j'ai pas des exos dans ce cours mais voila à un (c'est tout ce que j'ai trouvé)
prouver l'inégalité de Huygens
x de [0;pi/2[ 2sin(x)+tan(x)>=3x

Expert grade1 Nombre de messages : 428 Age : 28 Date d'inscription : 22/01/2014

Sur Wikipédia, j'ai trouvé la solution suivante (Solution que tout un chacun peut rédiger puisqu'elle ne fait appel qu'à la dérivée):

Démonstration par l'utilisation de la dérivée
Soit f fonction qui à tout x de $derivation 65c5b5ed2c227b81f59c76c86fb7c6d8$ , associe $derivation 6398e365c36de04ae125a9d92207789d$ .
Cette fonction est dérivable sur cet intervalle comme somme de fonctions dérivables. La fonction dérivée de f est la fonction f' qui à tout x de l'intervalle considéré associe :
$derivation Bb03b56b72d48c676cd3d43326e40bda$ .

Sur l'intervalle considéré, les inégalités suivantes sont vérifiées : $derivation 875eafef4615f1bacebbec8b1219389a$ et $derivation Fdf6ffdfa966a74ca135c6bcddf819a9$ .
Donc, $derivation 020b144af0f3ccc24c2661220795528d$ et la fonction f est croissante sur l'intervalle considéré.
On remarque l'égalité : $derivation E2a061a5ee974f36bf4280bac3962260$ par conséquent : $derivation A4bd6fc34a01a9786591a2ab689d4422$

Maître Nombre de messages : 238 Age : 27 Date d'inscription : 23/09/2012

à toi de poster un exo dans la dérivation ou les limites, le plus vite possible

Expert grade1 Nombre de messages : 428 Age : 28 Date d'inscription : 22/01/2014

1) f est continue sur R*- et sur R*+ , il reste à étudier la continuité sur 0.
lim (x->0-) f(x) = lim(x->0- ) f(x) =1=f(0) => f est continue en 0
2) f est dérivable sur R-* et dérivable sur R*+ , reste à étudier le point 0 encore une fois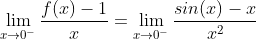
$derivation Gif$
Et : $derivation Gif$
cette limite a été mainte fois proposée dans le site, et dont le résultat n'est autre que 0
Alors f est bel et bien dérivable en 0, tq f'(0)=0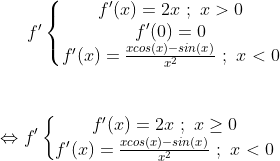
$derivation Gif.latex?f%27%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20f%27%28x%29%3D2x%5C%20%3B%5C%20x%3E0%20%5C%5C%20f%27%280%29%3D0%20%5C%5C%20f%27%28x%29%3D%20%5Cfrac%7Bxcos%28x%29-sin%28x%29%7D%7Bx%5E2%7D%5C%20%3B%5C%20x%3C0%20%5Cend%7Bmatrix%7D%5Cright.%20%5C%5C%20%5C%5C%20%5C%5C%20%5C%5C%20%5CLeftrightarrow%20f%27%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20f%27%28x%29%3D2x%5C%20%3B%5C%20x%5Cgeq0%20%5C%5C%20f%27%28x%29%3D%20%5Cfrac%7Bxcos%28x%29-sin%28x%29%7D%7Bx%5E2%7D%5C%20%3B%5C%20x%3C0%20%5Cend%7Bmatrix%7D%5Cright$
Sauf Erreur :p

Maître Nombre de messages : 238 Age : 27 Date d'inscription : 23/09/2012

à toi de poster un exo .

Expert grade1 Nombre de messages : 428 Age : 28 Date d'inscription : 22/01/2014

Pour remercier M. Legend_Crush pour sa solution, voici la solution proposée par l'auteur de l'exercice:

derivation Dariva11

Remarque: M. L_W_P avait fait une remarque, en ce qui concerne l'exercice de l'équation fonctionnelle de la page "Préparation aux olympiades", on a f(1) = 1 (je m'excuse de la faute de frappe) .

Débutant Nombre de messages : 3 Age : 27 Date d'inscription : 28/02/2014

salam ,
mr lwp tu peux m'expliquer comment tu trouve h'(x) en fonction de h(x) dans la 1er exo Sad

Rimy a écrit:: salam ,
mr lwp tu peux m'expliquer comment tu trouve h'(x) en fonction de h(x) dans la 1er exo

juste tawhid lma9am o khtazél ..

pr le 2éme exo :
Considère la fonction f(x)=2sin(x)+tan(x)-3x
Calcule f'(x)....
tu trouvera que f(x) est croissante sur [0.pi/2[
Ainsi :
f(x)>=f(0)=0
2sin(x)+tan(x)-3x >= 0
2sinx+tanx>=3x

» la derivation
» dérivation
» exo de dérivation.
» Dérivation !
» dérivation