- ayoubmath a écrit:
- exo 1
A et B deux matrices et X=poly caracteristique
montrer que X(A)=X(B) < ==> qqs k 0..n tr(A^k)=tr(B^k)
Je propose une solution:
On travaille sur
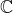
pour exploiter le fait que tout polynôme de degré

y admet

racines comptés par leurs ordre de multiplicité (Et ce même en travaillant sur

).
On utilise généralement le dernier théorème de cette page: http://fr.wikipedia.org/wiki/Relations_entre_coefficients_et_racines, avec
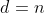
.
Et on garde les même notations que dans le lien, que ce soit pour les

racines
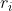
et les
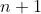
sommes
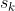
.
<==) On suppose que:
=\sum_{k=0}^{n}a_kX^k)
et
=\sum_{k=0}^{n}b_kX^k)
avec
^n)
.
On a
)
et
)
.
On a d'après l'hypothèse:
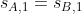
, ce qui suivant la première équation que
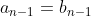
.
Et on démontre de proche en proche que
 : a_k=b_k)
.
Ce qui implique que
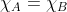
, comme voulu.
<==) Réciproquement, si
=\chi_B(X)=\sum_{k=0}^{n}a_k.X^k)
avec
^n)
.
On a clairement,
 :s_k=s_{A,k}=s_{B,k}=\text{Tr}(A^k)=\text{Tr}(B^k))
.
c/c) D'où l'équivalence, et la fin de la démonstration.
Sauf erreurs.
