DEVOIR N 3 OLYMPIADE PREMIERE SM 9 FEVRIER 2018

Bonjour ;

Exercice n° 1 .

1)

Pour k un nombre entier naturel ; on a : (1 - 1/3^(2k)) = (1 + 1/3^k) (1 - 1/3^k) ;
donc si k = 2^m ; on a : 2k = 2^(m + 1) : avec m un nombre entier naturel ;
donc : (1 - 1/3^(2^(m + 1))) = (1 + 1/3^(2^m)) (1 - 1/3^(2^m)) ;
donc : 1 + 1/3^(2^m) = (1 - 1/3^(2^(m + 1)))/(1 - 1/3^(2^m)) .

Soit A = produit(1 + 1/3^(2^m)) pour m allant de 0 à n un nombre entier naturel ;
donc : A = (1 - 1/3^(2^(0 + 1)))/(1 - 1/3^(2^0)) x ..... x (1 - 1/3^(2^(n + 1)))/(1 - 1/3^(2^n))
= (1 - 1/3^2)/(1 - 1/3) x (1 - 1/3^4)/(1 - 1/3^2) x ..... x (1 - 1/3^(2^(n + 1)))/(1 - 1/3^(2^n))
= (1 - 1/3^(2^(n + 1)))/(1 - 1/3)
= (3/2) x (1 - 1/3^(2^(n + 1))) .

La résultat de aymanemaysae pour l'exercice 1 est le bon. Pour l'exercice 3, je pense qu'on peut démontrer le résultat dans toute sa généralité:
Pour tout ensemble de points du plan, on peut montrer qu'il existe un cercle à l'intérieur duquel se trouvent points de , avec .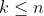
Les chiffres dans l'énoncé ( 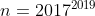et 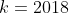) n'y sont que pour embrouiller les gens.