| | problème N°88 de la semaine (02/07/2007-08/07/2007) |  |
|
+23sami matrix stof065 yassine-mansouri ali 20/20 Alaoui.Omar In-16 khamaths Anas_CH colonel relena abdou20/20 badr kaderov abdelbaki.attioui Yalcin crazyharrypotter elhor_abdelali o0aminbe0o Oumzil aissa radouane_BNE samir 27 participants |
|
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: problème N°88 de la semaine (02/07/2007-08/07/2007)  Lun 02 Juil 2007, 21:57 Lun 02 Juil 2007, 21:57 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Lun 02 Juil 2007, 21:59 Lun 02 Juil 2007, 21:59 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 | |
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Lun 02 Juil 2007, 23:33 Lun 02 Juil 2007, 23:33 | |
| salut tout le monde
solution postée
je veux je peux
voici la solution d'aissa
salut samir
x et y>o z>o: alors x+y-2V(xy)>0 alors: (x+y)(x+z)(y+z)>=8xyz
on a: x+y+z=1 alors x+y=1-z , x+z=1-y et y+z=1-x
donc:
(1+x)(1+y)(1+z)=(x+z +y+z)(x+y +y+z)(x+y +x+z) >=
8(x+y)(x+z)(y+z)=8(1-x)(1-y)(1-z).
وقل ربي زدني علما | |
|
  | |
Oumzil
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 35
Date d'inscription : 28/08/2006
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 00:05 Mar 03 Juil 2007, 00:05 | |
| Sollution Postée ! à+ voici la solution d'Oumzil | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 12:37 Mar 03 Juil 2007, 12:37 | |
| salam alaikoum tout le monde
solution postée
(solution non trouvée parmis mes mails)(administration) | |
|
  | |
elhor_abdelali
Expert grade1

 Nombre de messages : 489 Nombre de messages : 489
Age : 62
Localisation : Maroc.
Date d'inscription : 24/01/2006
 | |
  | |
crazyharrypotter
Maître

 Nombre de messages : 289 Nombre de messages : 289
Age : 33
Localisation : maroc
Date d'inscription : 30/07/2006
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 13:16 Mar 03 Juil 2007, 13:16 | |
| solution postèe
voici la solution de crazyharypotter
x .y .z trois rèel strictement positifs et z+y+x=1
==> 0<x<1 et 0<y<1 et 0< z<1
==> 1<x+1<2 et 0<1-x<1 et 1<y+1<2 et 0<1-y<1 et 1<z+1<2 et 0<1-z<1
==> 1<x+1<2 et 1<1/(1-x) et 1<y+1<2 et 1<1/(1-y) et 1<z+1<2 et 1<1/(1-z)
==> 2=<x+1/1-x et 2=<y+1/1-y et 2=<z+1/1-z
==> 8=<(x+1)(y+1)(z+1)/(1-x)(1-y)(1-z) on a [ 0<1-x<1 et 0<1-y<1 et 0<1-z<1 ==>0<(1-x)(1-y)(1-z)]
==> 8(1-x)(1-y)(1-z)=<(x+1)(y+1)(z+1)
merci | |
|
  | |
Yalcin
champion de la semaine
Nombre de messages : 21
Date d'inscription : 19/09/2005
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 13:32 Mar 03 Juil 2007, 13:32 | |
| solution postée
voici la solution de yalcin
posons u(x)= [(1+x)/(1-x)]
posons f(x,y,z) = u(x).u(y).u(z)
posons g(x,y)=f(x,y,1-(x+y)) c'est cette fonction qu'on veut minorer
or diff(g(x,y),x)=2(y-1+2x)(1+y)/((x+y)²(x-1)²)
d'où on obtient avec un tableau de variation qu'on a un minimum de la fonction g(x,y) en x=(1-y)/2 ,et on a g(x,y)>=g((1-y)/2,y)
or g((1-y)/2,y)=(y-3)²/(1-y²) , posons t(y)=g((1-y)/2,y)
or diff(t(y),y)=2(3-y)(3y-1)/((y²-1)²) ,d'où avec un tableau de variation , on obtient un minimum de la fonction t(y) en y=1/3
d'où t(y)>=t(1/3) , comme g(x,y)>=t(y) ,d'où g(x,y)>=t(1/3) , or t(1/3)=8
finalement on obtient : g(x,y)>=8 ,d'où f(x,y,z)>=8 ,avec x+y+z=1
et finalement on obtient : (1+x)(1+y)(1+z)>=8(1-x)(1-y)(1-z) | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 13:49 Mar 03 Juil 2007, 13:49 | |
| Bonjour
Solution postée
voici la solution d'abdelbaki.attioui
Il est clair que 0<x,y,z<1
On pose : 2a=1-x , 2b=1-y, 2c=1-z ==> 0<a,b,c<1 et a+b+c=1
L'inégalité devient: (1-a)(1-b)(1-c)>=8abc
<==> 1-a-b+ab-c+ac+bc-abc>=8abc
<==> ab+bc+ac>=9abc
<==> 1/a+1/b+1/c>=9.
Mais il est bien connu que (a+b+c)(1/a+1/b+1/c)>=9
A+ | |
|
  | |
kaderov
Maître

 Nombre de messages : 89 Nombre de messages : 89
Age : 56
Localisation : Casablanca
Date d'inscription : 03/07/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 15:20 Mar 03 Juil 2007, 15:20 | |
| Salut
Solution postée
voici la solution de Kaderov
Posons a=x+y b=y+z c= x+z
On a alors : 2x+y+z=1+x= a+c; x+2y+z=1+y =a+b; x+y+2z=1+z=c+b &
1-x=y+z=b ; 1-y=x+z=c ; 1-z=x+y=a
L¡¯in¨¦galit¨¦ devient :
( a+b)( b+c)( c+a ) ¡Ý 8abc
Or a+b¡Ý 2¡Ìab ; a+c ¡Ý 2¡Ìac ; b+c ¡Ý 2¡Ìbc
En faisant le produit des 3 in¨¦galit¨¦s nous obtenons l¡¯in¨¦galit¨¦ d¨¦sir¨¦e | |
|
  | |
badr
Expert sup

 Nombre de messages : 1408 Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
 | |
  | |
Invité
Invité
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 20:16 Mar 03 Juil 2007, 20:16 | |
| solution pstée
voici la solution de neutrino
slt
puisque x+y+z=1
(1+x)(1+y)(1+z)= ( x+y+z+x)( x+y+z+y)( x+y+z+z) = [ (x+y)+(z+x)][(x+y) + (z+y) ][ (x+z)+ (y+z)] >= ( on utilise le fait que a+b>=2rac(ab) )8( x+y)(y+z)(z+x) = 8(1-z)(1-x)(1-y)
Dernière édition par le Ven 06 Juil 2007, 18:44, édité 1 fois |
|
  | |
abdou20/20
Expert sup

 Nombre de messages : 713 Nombre de messages : 713
Age : 33
Localisation : rabat
Date d'inscription : 12/06/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mar 03 Juil 2007, 21:03 Mar 03 Juil 2007, 21:03 | |
| ATTENTION
tu dois poster ta solution par e-mail | |
|
  | |
relena
Expert sup

 Nombre de messages : 701 Nombre de messages : 701
Date d'inscription : 06/11/2006
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mer 04 Juil 2007, 10:57 Mer 04 Juil 2007, 10:57 | |
| Bonjour !
Solution postée
voici la solution de relena
Bonjour ! Voici ma réponse pour le problème de semaine N° 88 :
(x,y,z) £ IR*+ tels que x+y+z = 1
On pose :
A = (1+x) (1+y) (1+z) = (2x+y+z) (2y+x+z) (2z+x+y) car x+y+z = 1
B = 8(1-x) (1-y) (1-z) = 8 (x+y) (y+z) (z+x) car x+y+z = 1
X = x+y ; Y = y+z et Z = z+x
X+Y >= 2racine(X.Y)
Y+Z >= 2racine(Y.Z)
Z+X >= 2racine(Z.X)
D'où (X+Y) (Y+Z) (Z+X) >= 8XYZ
donc (2x+y+z) (2y+x+z) (2z+x+y) >= 8 (x+y) (y+z) (z+x)
D'où A >= B et c'est ce qu'on veut
Life is nothing without hope. Relena | |
|
  | |
colonel
Expert grade1

 Nombre de messages : 498 Nombre de messages : 498
Age : 33
Localisation : base millitaire
Date d'inscription : 10/06/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mer 04 Juil 2007, 11:39 Mer 04 Juil 2007, 11:39 | |
| salut .
solution postéé
voici la solution de colonel
je suis partie d'un exo qui demande de montrer que pour x>0, y>0 et z>0, on a :
(x+y)(y+z)(x+z) >= 8xyz
on a (x+y)(y+z)(x+z)-8xyz = xz²+zy²+yz²+zx²+xy²+yx²-6xyz
= xz²-xyz + zy²-xyz + yz²-xyz + zx²-xyz + xy²-xyz + yx²-xyz
= xz(z-y) + zy(y-x) + yz(z-x) + zx(x-y) + xy(y-z) + xy(x-z)
= x(z-y)² + z(y-x)² + y(z-x)² qui est positif ou nul
en appliquant ce résultat avec x = 1-a ; y = 1-b ; z = 1-c et donc a+b+c = 1
on a donc x+y = 2-a-b =1+c ; x+z = 2-a-c = 1+b ; y+z = 2-b-c = 1+a
on obtient bien (1+a)(1+b)(1+c) >= 8(1-a)(1-b)(1-c)
Dernière édition par le Jeu 05 Juil 2007, 12:17, édité 2 fois | |
|
  | |
Anas_CH
Maître

 Nombre de messages : 218 Nombre de messages : 218
Age : 33
Date d'inscription : 19/01/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mer 04 Juil 2007, 13:41 Mer 04 Juil 2007, 13:41 | |
| السلام عليكم ورحمة الله وبركاته
SOLUTION POSTéE
voici la solution d'anass
On a : x>0 , y>0, z>0 et x+y+z=1
Donc : 0<x<1 et 0<y<1 et 0<z<1 => (1-x)(1-y)(1-z)>0 =>(1-x)(1-y)(1-z)≠0
[(1+x)(1+y)(1+z)]/[(1-x)(1-y)(1-z)]
= [(1+x)/(1-y)]*[(1+y)/(1-z)]*[(1+z)/(1-x)]
= [(x+z)/(x+z)+(x+y)/(x+z)]*[(x+y)/(x+y)+(y+z)/(x+y)]*[(y+z)/(y+z)+(z+x)/(y+z)]
= (1+(x+y)/(x+z)) (1+ (z+x)/(y+z)) (1+ (y+z)/(x+y))
posant (x+y)=a et (x+z)=b et (y+z)=c
on a : [(1+x)(1+y)(1+z)]/[(1-x)(1-y)(1-z)]=(1+a/b)(1+b/c)(1+c/a)
=(1+b/c+a/b+a/c)(1+c/a)
=1+b/c+a/b+a/c+b/a+c/b+c/a+1
on sait que a et b et c sont strictement positive
donc a/b+b/a≥2 et a/c+c/a≥2 et c/b+b/c≥2
alors 1+b/c+a/b+a/c+b/a+c/b+c/a+1≥8
<=> [(1+x)(1+y)(1+z)]/[(1-a)(1-b)(1-c)] ≥8
et enfin on a
(1+x)(1+y)(1+z) ≥8(1-a)(1-b)(1-c) | |
|
  | |
khamaths
Maître
Nombre de messages : 98
Date d'inscription : 17/03/2006
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mer 04 Juil 2007, 18:08 Mer 04 Juil 2007, 18:08 | |
| Bonjour
Solution postée
voici la solution de khamaths
Bonjour Samir
Il est clair que x ; y et z ¤ ]0;1[ =I ( x+y+z =1)
le problème revient à montrer que :
P = (1+x)/(1-x)*(1+y)/(1-y)*(1+z)/(1-z) >= 8
considérons la fonction : f(x) = ln[ (1+x)/(1-x) ] : x ¤ ]0;1[=I
f est définie et de classe C² sur I et on a : f '' (x) = 4x/(1-x²)² > 0 sur I ====> f est convexe sur I
=====> f(x) + f(y) + f(z) >= 3 f[ (x+y+z)/3]
====> f(x) +f(y) +f(z) >= 3f(1/3)=3ln2
====> ln P >= ln 8
===> P >= 8
===> (1+x)(1+y)(1+z) >= 8 (1-x)(1-y)(1-z) | |
|
  | |
In-16
Habitué
 Nombre de messages : 13 Nombre de messages : 13
Age : 33
Date d'inscription : 28/02/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mer 04 Juil 2007, 20:03 Mer 04 Juil 2007, 20:03 | |
| "solution postée"
voici la solution de Ln-16
salam
on, a x+y+z=1 donc x<1 e y<1 e z<1 puiskils sont strictement positifs
(1-x)+(1-y)>=2rac(1-x)* rac (1-y)
(1-x)+(1-z)>=2rac(1-x)*rac(1-z)
(1-z)+(1-y)>=2rac(1-y)*rac(1-z)
alors (2-x-y)(2-y-z)(2-z-x) >= 8(1-x)(1-y)(1-z)
2-x-y= 1+1-x-y=1+z la mm chose pr le 2 autres
dou
(1+x)(1+z)(1+y)>=8(1-x)(1-y)(1-z)
* vx dire multiplié par
In-16 | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Mer 04 Juil 2007, 23:19 Mer 04 Juil 2007, 23:19 | |
| solution postée voici la solution de Alaoui.Omar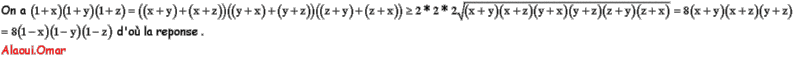 | |
|
  | |
ali 20/20
Maître

 Nombre de messages : 239 Nombre de messages : 239
Date d'inscription : 01/07/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Jeu 05 Juil 2007, 12:00 Jeu 05 Juil 2007, 12:00 | |
| Sollution postée
(solution non trouvée parmis mes mails)(administration) | |
|
  | |
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Jeu 05 Juil 2007, 13:46 Jeu 05 Juil 2007, 13:46 | |
| Solution postée  voici la solution de yassine-mansouriOn va poser voici la solution de yassine-mansouriOn va poser
a=x+z a+b=x+1 (a,b,c>0)
b=x+y b+c=y+1
c=y+z c+a=z+1
Sachant que
(a+b)(b+c)(c+a)>=8abc (*)
Alors
(x+1)(y+1)(z+1)>=(x+y)(x+z)(z+y)
On a x+y+z=1
Alors
x+y=1-z et x+z=1-y et y+z=1-x
D’où
(x+1)(y+1)(z+1)>= (1-x)(1-y)(1-z)
Démonstration de l’inéquation (*) :
a/b+b/a+a/c+c/a+b/c+c/b>=6
=>a²b+b²a+a²c+c²a+b²c+c²b>=6abc
=>a²b+b²a+a²c+c²a+b²c+c²b+2abc>=8abc
=>(a+b)(b+c)(c+a)>=8abc | |
|
  | |
stof065
Expert sup

 Nombre de messages : 540 Nombre de messages : 540
Age : 34
Date d'inscription : 01/02/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Jeu 05 Juil 2007, 20:42 Jeu 05 Juil 2007, 20:42 | |
| solution postée
voici la solution de stof065
sllttt
on a x+y+z=1
(1+x)(1+y)(1+z)=(2x+y+z)(2y+z+x)(2z+x+y)
=((x+y)+(x+z))((y+z)+(y+x))((z+y)+(z+x))
on (implique a²+b²>=2ab)
(1+x)(1+y)(1+z)=((x+y)+(x+z))((y+z)+(y+x))((z+y)+(z+x))
>=8rac[(x+y)²(y+z)²(z+x)²]=8(x+y)(y+z)(z+x)
=8(1-x)(1-y)(1-z) (car x+y+z=1)
SToF065
a+ | |
|
  | |
matrix
Maître

 Nombre de messages : 115 Nombre de messages : 115
Age : 34
Date d'inscription : 03/07/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Ven 06 Juil 2007, 12:31 Ven 06 Juil 2007, 12:31 | |
| "solution postée"
(solution non trouvée parmis mes mails)(administration) | |
|
  | |
sami
Expert sup

 Nombre de messages : 1455 Nombre de messages : 1455
Age : 34
Localisation : N/A
Date d'inscription : 01/02/2007
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  Ven 06 Juil 2007, 19:24 Ven 06 Juil 2007, 19:24 | |
| solution postée
voici la solution de sami
salut
je suis partie d'un exo qui demande de montrer que pour x>0, y>0 et z>0, on a :
(x+y)(y+z)(x+z) >= 8xyz
on a (x+y)(y+z)(x+z)-8xyz = xz²+zy²+yz²+zx²+xy²+yx²-6xyz
= xz²-xyz + zy²-xyz + yz²-xyz + zx²-xyz + xy²-xyz + yx²-xyz
= xz(z-y) + zy(y-x) + yz(z-x) + zx(x-y) + xy(y-z) + xy(x-z)
= x(z-y)² + z(y-x)² + y(z-x)² qui est positif ou nul
en appliquant ce résultat avec x = 1-a ; y = 1-b ; z = 1-c et donc a+b+c = 1
on a donc x+y = 2-a-b =1+c ; x+z = 2-a-c = 1+b ; y+z = 2-b-c = 1+a
on obtient bien (1+a)(1+b)(1+c) >= 8(1-a)(1-b)(1-c) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007) Sujet: Re: problème N°88 de la semaine (02/07/2007-08/07/2007)  | |
| |
|
  | |
| | problème N°88 de la semaine (02/07/2007-08/07/2007) |  |
|
