| | Suites convergente <==> Suite de Cauchy |  |
|
|
| Auteur | Message |
|---|
Weierstrass
Expert sup
 Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
| | Sujet: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 13:54 | |
| Montrer qu'une suite r_n converge si et ssi elle est une suite de cauchy ie  | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 13:58 | |
| salut mahdi
on sait que
Toute suite convergente est une suite de Cauchy. et
Toute suite de Cauchy est bornée. | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:00 | |
| | |
|
| | |
Weierstrass
Expert sup
Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:07 | |
| on suppose qu'on sait rien ! on doit le demontrer avec ces données | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:16 | |
|
Fixons <IMG height=33 alt="$ \varepsilon >0$" src="http://ljk.imag.fr/membres/Bernard.Ycart/mel/sr/img92.gif" width=48 align=middle border=0> . Il existe un entier 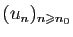 à partir duquel | U_n-l|<e /2 et |U_(n+k)<e/2 et pour tt 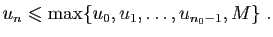 et pour tout  :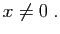
Dernière édition par le Dim 28 Oct 2007, 14:23, édité 3 fois | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:19 | |
| on a utilisant l'inégalité triangulaire | |
|
| | |
Weierstrass
Expert sup
Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:22 | |
| - badr a écrit:
<SPAN class=MATH>Fixons <IMG height=33 alt="$ \varepsilon >0$" src="http://ljk.imag.fr/membres/Bernard.Ycart/mel/sr/img92.gif" width=48 align=middle border=0> . Il existe un entier 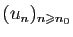à partir duquel 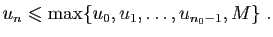et pour tout :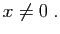
je l'ai vu oui http://ljk.imag.fr/membres/Bernard.Ycart/mel/sr/node9.html | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:24 | |
| oui mais pour au terminal est une thoereme admit | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:35 | |
| donc apres cette demontration est ce que peut dire que les suite U_n et U_n+k sont adjecents? | |
|
| | |
Weierstrass
Expert sup
Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:38 | |
| tu dois montrer que l'une est croissante l'autre est decroissante d'abord puis tu passes a la limite , bon tu sais quoi je crois pas que t'as choisi le bon chemin | |
|
| | |
badr
Expert sup
Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
| | Sujet: Re: Suites convergente <==> Suite de Cauchy Dim 28 Oct 2007, 14:39 | |
| - Mahdi a écrit:
- tu dois montrer que l'une est croissante l'autre est decroissante d'abord puis tu passes a la limite , bon tu sais quoi je crois pas que t'as choisi le bon chemin
pour quel chemein tu parle? | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Suites convergente <==> Suite de Cauchy | |
| |
|
| | |
| | Suites convergente <==> Suite de Cauchy | |
|
