Olympiade sur réseau

hadakchy li katbyne je c rien

voici une eq fonctionnel

la solution va etre postée d ici 45min
allez courage c est tres facile et tres elementaire pour quelqu un qui va passer les olympiades

paheli a écrit:

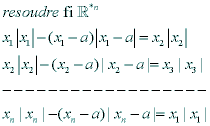c t un systeme

voici un exercice un peu facile:
annie possede u nombre de sucettes:si elle les range par 5 ils lui en restent 3.si elle les range par 7 ils lui en restent 2.sachant que le nombres de sucettes appartient a l intervalle [100,200] etudiez les cas possibles.

tu doit avoir vu ti3dad!

slt!
alors les olympiades sont pour vendredi! qui est qualifié parmi vous et combien dans votre ville sont qualifiés?

paheli a écrit:

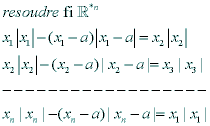fait une sommation des cote s des equation et tu vierra le resultat plus facil

ps les sujet est deja poste

memath a écrit:

voici une eq fonctionnel

la solution va etre postée d ici 45min
allez courage c est tres facile et tres elementaire pour quelqu un qui va passer les olympiades

le resultat est f(x)=x
on suppose que f(x))#x ===>f(x)>x ou f(x)<x avec f est croissante donc ff(x)>f(x)>x ou f(f(x))<f(x)<x===>f(f(x))#x ce qui est absurbe CQFD

je vais poster un nouveau exo

soit a,b,c des reels strictement positifs tel que: ab+bc+ca>= a+b+c>0 .demontrer que a+b+c>=3

voila un autre
determiner tt les nombres a ,b et c de N* tel que 1/a+1/b+1/c=1

pour cet exo voici ce que jai trouver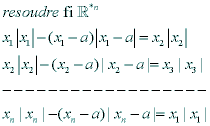



en sommant tous les lignes on va trouver

(x1-a)./(x1-a)/+.....+(xn-a)./(xn-a)/=0

on remarque dapres cette derniere equaation que
(a.a.....a) est une solution pour ce systeme
comment je peux continuer svp

paheli a écrit:

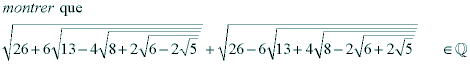6+rav5 = (rac5+1)²
......

oui cest ca et on va continuer avec les autre de la meme facon cest long

je pense que ta oublier un 2 mais ce nest pas un grang probleme
6+2rav5 = (rac5+1)²

on continue:

remarquer que
f(0)=0
f(2x)=2f(sinPI/2*x)
(x-y)f(x+y)+(x+y)f(x-y)=0

faut remarquer plutot que :
on choisissant y=2 et x=-x que :
f(-2x)=f(sin(-pi/2*x+pi))+f(sin(-pi/2*x-pi))=2f(sin(pi/2*x))=f(2x)
ce qui signifit que f est paire.
et dans la deuxieme condition si on choisit x=0 on aura :
f(-y²)=yf(-y)-yf(y)=y(f(-y)-f(y))=0
donc f coincide avec la fonction nul sur R- et puisque f est paire c est donc que f est la fonction nul sur R.
donc f(x)=0.
et reciproquement ca marche

Trouver tous les couples d'entiers strictement positifs(a,b)tels que:

a²⁄ (2ab²-b³+1) soit un entier soit strictement positif.

Trouver toutes les fonctions f : (de R vers R), où R désigne l’ensemble des réels,vérifiant
(f(x)+f(z))(f(y)+f(t))=f(xy-zt)+f(xt+yz)
Pour tous les x,y,z ,t de R

Soient x,y,z trois réels strictement positifs tel que x² + y² + z² = 1
Démontrez que :
1/(1-xy) + 1/(1-yz) + 1/(1-xz) < 9/2

Trouver tous les pôlynomes P(x) à coefficients réels qui vérifient l'égalité:

P(a-b)+P(b-c)+P(c-a)=2P(a+b+c)

pour tous réels a,b,c tels que: ab+bc+ca=0