| | Une caractérisation de l'identité de IN |  |
|
+3wiles mathman abdelbaki.attioui 7 participants |
| Auteur | Message |
|---|
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Une caractérisation de l'identité de IN Sujet: Une caractérisation de l'identité de IN  Mar 25 Juil 2006, 13:51 Mar 25 Juil 2006, 13:51 | |
| Soit f: IN --> IN une fonction telle que pour tous m, n de IN
(m² + n)² est divisible par f²(m) +f(n).
Montrer que f(n) = n pour tout n de IN. | |
|
  | |
mathman
Modérateur
 Nombre de messages : 967 Nombre de messages : 967
Age : 35
Date d'inscription : 31/10/2005
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Mar 25 Juil 2006, 14:17 Mar 25 Juil 2006, 14:17 | |
| Liste courte 2004 encore.
C'est un joli problème. (mais on peut trouver des solutions arbitrairement laides si on ne fait pas attention) | |
|
  | |
wiles
Expert sup

Nombre de messages : 501
Age : 34
Localisation : khouribga
Date d'inscription : 03/04/2007
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Ven 15 Juin 2007, 09:04 Ven 15 Juin 2007, 09:04 | |
| slt codex00
ca se voit que la fonction que tu a trouve ne fonctionne pas (remplace et tu verra)
je crois que le bleme est dans ton premier resultat (pour m=n=0 on a f(0)^2+f(0) divise 0 mais ca ne veut pas dire que f(0)^2+f(0) est egale a 0 puisque tout nombre de N divise 0) | |
|
  | |
wiles
Expert sup

Nombre de messages : 501
Age : 34
Localisation : khouribga
Date d'inscription : 03/04/2007
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Ven 15 Juin 2007, 09:07 Ven 15 Juin 2007, 09:07 | |
| en plus de ca la fonction est definie de N* vers N* t'a pas donc le droit de parler de f(0) | |
|
  | |
mathman
Modérateur
 Nombre de messages : 967 Nombre de messages : 967
Age : 35
Date d'inscription : 31/10/2005
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Ven 15 Juin 2007, 09:07 Ven 15 Juin 2007, 09:07 | |
| Voici le message dont parle wiles : - codex00 a écrit:
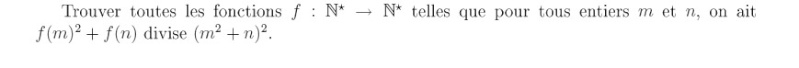
k(f(m)²+f(n))=(m²+n)² k€Z*
on pose m=n=0
f(0)=0
on pose m=0
f(n)=n²/k
Correction svp  (posté ici.) | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Ven 15 Juin 2007, 11:24 Ven 15 Juin 2007, 11:24 | |
| You're right, sorry, I'll try again  | |
|
  | |
FOUAD80
Féru

 Nombre de messages : 60 Nombre de messages : 60
Age : 44
Localisation : VIVE LE MAROC
Date d'inscription : 29/01/2007
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Sam 16 Juin 2007, 21:37 Sam 16 Juin 2007, 21:37 | |
| | |
|
  | |
le roi des maths
Féru

Nombre de messages : 65
Date d'inscription : 16/06/2007
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Dim 17 Juin 2007, 00:07 Dim 17 Juin 2007, 00:07 | |
| j'espere que vous dependerez de votre capacité pas d'un logiciel , la^prochaine fois ..[/img] | |
|
  | |
le roi des maths
Féru

Nombre de messages : 65
Date d'inscription : 16/06/2007
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Dim 17 Juin 2007, 00:09 Dim 17 Juin 2007, 00:09 | |
| | |
|
  | |
FOUAD80
Féru

 Nombre de messages : 60 Nombre de messages : 60
Age : 44
Localisation : VIVE LE MAROC
Date d'inscription : 29/01/2007
 | |
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  Sam 23 Juin 2007, 20:04 Sam 23 Juin 2007, 20:04 | |
| voila ma solution
on peut facilement trouver que
f(n)=n²/d_n et f(n-1)+1=n²/d'_n
=> n²/d_n +1=(n+1)²/d'_n+1 pour tout n de N
=> d_n=d'_n=n
=> f(n)=n | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Une caractérisation de l'identité de IN Sujet: Re: Une caractérisation de l'identité de IN  | |
| |
|
  | |
| | Une caractérisation de l'identité de IN |  |
|
