| | Préparation aux Olympiades 2013/2014 |  |
|
+6L-W-P AYb mt2sr galillee56 Humber legend-crush 10 participants |
|
| Auteur | Message |
|---|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Préparation aux Olympiades 2013/2014 Sujet: Préparation aux Olympiades 2013/2014  Ven 27 Sep 2013, 20:02 Ven 27 Sep 2013, 20:02 | |
| J'ouvre Donc un sujet destiné à la preparation aux olympiades pour l'année de 2013/2014. (Priere de numéroter les Exercices) .Je commence: Exercice 1:Calculer en fonction de n:  .  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Mar 01 Oct 2013, 21:29 Mar 01 Oct 2013, 21:29 | |
| Soir E(√k)=t donc t²=<k<t²+2t+1 donc le nombre de parties entières ayant la même valeur est t²+2t+1-t²=2t+1. Donc S=(2*1+1)*E(√3)+(2*2+1)*E(√8 )+...+E(√n)(2E(√n)+1). Donc, avec cette écriture, on ne considère que les E(√k) tels que k=m²-1, il faudra donc considérer les autres E(√k) distinctement. Ainsi : avec E(√n)²=<n< (E(√n)+1)² :   S'il y a des remarques, on peut discuter, je n'ai pas pu tout détailler dans la rédaction. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Mar 01 Oct 2013, 22:15 Mar 01 Oct 2013, 22:15 | |
| Exercice 2:
Trouvez tous les polynômes R(x) à coefficients réels satisfaisants :
(x-2010)R(x+67)=xR(x) pour tout entier x | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Lun 11 Nov 2013, 22:50 Lun 11 Nov 2013, 22:50 | |
| Désolé pour le retard et je ne sais pas si ce raisonnement est juste:
-on prenant x=0 on trouve R(64)=0
-Et on peut facilement déduire par récurrence que R(64k)=0 quelque soit k appartenant à N*
Donc R a une infinité de racines , ce qui veut dire que R est le polynôme nul.
Donc R(x)=0 | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Lun 11 Nov 2013, 22:55 Lun 11 Nov 2013, 22:55 | |
| - legend-crush a écrit:
- Désolé pour le retard et je ne sais pas si ce raisonnement est juste:
-on prenant x=0 on trouve R(64)=0
-Et on peut facilement déduire par récurrence que R(64k)=0 quelque soit k appartenant à N*
Donc R a une infinité de racines , ce qui veut dire que R est le polynôme nul.
Donc R(x)=0 remarque et indice 2010=67*30  | |
|
  | |
mt2sr
Maître

 Nombre de messages : 104 Nombre de messages : 104
Date d'inscription : 16/01/2006
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Mar 12 Nov 2013, 22:38 Mar 12 Nov 2013, 22:38 | |
| | |
|
  | |
mt2sr
Maître

 Nombre de messages : 104 Nombre de messages : 104
Date d'inscription : 16/01/2006
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Mer 13 Nov 2013, 11:56 Mer 13 Nov 2013, 11:56 | |
| je crois qu'on a le résultat suivant :tout polynôme périodique est constante 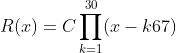 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Mer 13 Nov 2013, 13:13 Mer 13 Nov 2013, 13:13 | |
| - galillee56 a écrit:
- legend-crush a écrit:
- Désolé pour le retard et je ne sais pas si ce raisonnement est juste:
-on prenant x=0 on trouve R(64)=0
-Et on peut facilement déduire par récurrence que R(64k)=0 quelque soit k appartenant à N*
Donc R a une infinité de racines , ce qui veut dire que R est le polynôme nul.
Donc R(x)=0 remarque et indice 2010=67*30  j'avais confondu 64 et 67 dans ce que j'ai ecris | |
|
  | |
AYb
Débutant
 Nombre de messages : 6 Nombre de messages : 6
Age : 26
Localisation : Casablanca
Date d'inscription : 15/11/2013
 | |
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Ven 15 Nov 2013, 23:36 Ven 15 Nov 2013, 23:36 | |
| Je propose comme Exercice 3: | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Dim 17 Nov 2013, 16:10 Dim 17 Nov 2013, 16:10 | |
| solution exercice 3
Une application directe de Cauchy Schwartz
http://latex.codecogs.com/gif.latex?%28k+a_%7B1%7D%29%28k+a_%7B2%7D%29.......%28k+a_%7Bn%7D%29%5Cgeq%20%28%5Csqrt%5Bn%5D%7Bk%7D*%5Csqrt%5Bn%5D%7Bk%7D*......%5Csqrt%5Bn%5D%7Bk%7D+%5Csqrt%5Bn%5D%7Ba_%7B1%7Da_%7B2%7D....a_%7Bn%7D%7D%29%5E%7Bn%7D%20%5CRightarrow%20%5Cprod_%7Bi%3D1%7D%5E%7Bi%3Dn%7D%28k+a_%7Bi%7D%29%5Cgeq%28k+n%29%5E%7Bn%7D
Dernière édition par L-W-P le Dim 17 Nov 2013, 19:53, édité 1 fois | |
|
  | |
Kenichi
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 26
Localisation : Casa
Date d'inscription : 16/11/2013
 | |
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Dim 17 Nov 2013, 21:26 Dim 17 Nov 2013, 21:26 | |
|  et déduire!! | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Dim 17 Nov 2013, 21:29 Dim 17 Nov 2013, 21:29 | |
| - L-W-P a écrit:
- solution exercice 3
Une application directe de Cauchy Schwartz
http://latex.codecogs.com/gif.latex?%28k+a_%7B1%7D%29%28k+a_%7B2%7D%29.......%28k+a_%7Bn%7D%29%5Cgeq%20%28%5Csqrt%5Bn%5D%7Bk%7D*%5Csqrt%5Bn%5D%7Bk%7D*......%5Csqrt%5Bn%5D%7Bk%7D+%5Csqrt%5Bn%5D%7Ba_%7B1%7Da_%7B2%7D....a_%7Bn%7D%7D%29%5E%7Bn%7D%20%5CRightarrow%20%5Cprod_%7Bi%3D1%7D%5E%7Bi%3Dn%7D%28k+a_%7Bi%7D%29%5Cgeq%28k+n%29%5E%7Bn%7D C'est pas holder (pa caushy)? | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Ven 03 Jan 2014, 20:04 Ven 03 Jan 2014, 20:04 | |
| Exercice 4:trouver toutes les fonctions de R vers R, tel que: 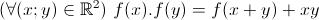 | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 27
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Ven 03 Jan 2014, 20:31 Ven 03 Jan 2014, 20:31 | |
| - Indication:
1-f(0)=1
2-f(1)=0 ou f(-1)=0
3-f(x)=1-x ou f(x)=x+1
| |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Ven 03 Jan 2014, 21:16 Ven 03 Jan 2014, 21:16 | |
| calculer f(0) on trouva que f(0)=0 ou f(0)=1 or f(x)=0 n'a pas de solution
alors f(0)=1
puis on calcule f(1).f(-1)=0
et remplaçant on trouvera f(x)= 1-x ou f(x)=x+1
je vais poster le 5 exercice dans les plus brefs délais | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 00:10 Sam 04 Jan 2014, 00:10 | |
| Exercie 5: Déterminer les fonctions de R--->R telles que, pour tous réels x,y: 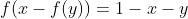 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 00:50 Sam 04 Jan 2014, 00:50 | |
| y=0 et x=a+f(0) --> f(a)=1-f(0)-a
on pose c=1-f(0) donc f(x)=c-x
en remplacent on trouve 2c-x-y=1-x-y ce qui assure que c=1/2
donc f(x)=1/2-x
| |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 00:56 Sam 04 Jan 2014, 00:56 | |
| Exo 6:
determiner toutes les fonctions de R vers R tq:
xf(x+xy)=xf(x)+f(x²)f(y) | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 13:03 Sam 04 Jan 2014, 13:03 | |
| on va avoir deux cas
cas 1 f(1)=0 et f(1)=0 alors par une simple manipulation f(x)=0
cas 2 f(1)=1 et f(-1)=-1
remplaçant y=-1 on va avoir f(x^2)=xf(x)
remplaçant y=x-1 et en utilisant les deux égalités résultées on va trouver f(x)(x-1-f(x-1))=0
ce qui donne que f(x)=x
Dernière édition par L-W-P le Sam 04 Jan 2014, 13:12, édité 2 fois | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 13:04 Sam 04 Jan 2014, 13:04 | |
| j'attends votre confirmation pour passer au 7 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 13:32 Sam 04 Jan 2014, 13:32 | |
| oui f(x)=x ou f(x)=0 , à toi  | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 13:42 Sam 04 Jan 2014, 13:42 | |
| EXO 7
déterminer toutes les fonctions de N----N
telles que pour tous x,y de N on a
f(f(n)+f(m))=m+n | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  Sam 04 Jan 2014, 13:57 Sam 04 Jan 2014, 13:57 | |
| Remarquer que si f(m)=f(n) alors m+n=f(f(m)+f(n))=f(f(n)+f(n))=2n --> m=n
ce qui assure que f est bel est bien injective.
on remarque d'ailleurs que 2n=n+1+n-1=f(f(n+1)+f(n-1)) et 2n=n+n=f(f(n)+f(n))
donc f(f(n+1)+f(n-1))=f(f(n)+f(n)) et donc vu que f est injective f(n+1)+f(n-1)=f(n)+f(n)
d'ou f(n+1)-f(n)=f(n)-f(n-1) (donc f a une pente constante ) d'ou f affine
donc f(n)=an+b et on peut facilement déduire que la seule solution est f(n)=n
on peut aussi démontrer que f(n)=n par réccurence forte puisque f(n+1)=2f(n)-f(n-1)=2n-n+1=n+1 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation aux Olympiades 2013/2014 Sujet: Re: Préparation aux Olympiades 2013/2014  | |
| |
|
  | |
| | Préparation aux Olympiades 2013/2014 |  |
|
