| | exercice )5(: |  |
|
|
| Auteur | Message |
|---|
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: exercice )5(: Sujet: exercice )5(:  Mar 05 Aoû 2008, 20:34 Mar 05 Aoû 2008, 20:34 | |
| exercice )(: soit f:[0,1]-->IR une fonction continue satisfaisant xf(y)+yf(x)=<1 pour tout x,y£[0,1].
*1/montrer que: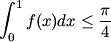 *2/donner un exemple d'égalité. *2/donner un exemple d'égalité.
Dernière édition par boukharfane radouane le Mar 05 Aoû 2008, 21:14, édité 1 fois | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 21:12 Mar 05 Aoû 2008, 21:12 | |
| - boukharfane radouane a écrit:
- exercice )(:
soit f:[0,1]-->IR une fonction continue satisfaisant xf(y)+y(x)=<1 pour
tout x,y£[0,1].
*1/montrer que:
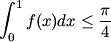
*2/donner un exemple d'égalité. je pense que c'est xf(Y)+yf(X)=<1 ? | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 21:13 Mar 05 Aoû 2008, 21:13 | |
| oui désolé c'est réctifié!merci. | |
|
  | |
exodian95
Modérateur
 Nombre de messages : 246 Nombre de messages : 246
Age : 24
Date d'inscription : 27/06/2008
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 21:40 Mar 05 Aoû 2008, 21:40 | |
| 2*) exemple d'egalité: f(x)=(sqrt(1-x²))/2 | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 21:55 Mar 05 Aoû 2008, 21:55 | |
| soit (x,y)=(sin(u),cos(u)) avec u decrit [o,Pi/2]
On remarque integ_{o^pi/2}cos(u)f(sin(u))du=integ_{o^1}f(t)dt=integ_{o^pi/2}sin(u)f(cos(u))
alors integronc linegalité entre O et pi/2 On aura : 2integ{O^1}f(t)dt=<pi/2
d'ou integ (O..Pi/2) f(t)dt=<Pi/4. se
cas degalité x--> 1/(1+t²) marche bien je pense.
A+ | |
|
  | |
exodian95
Modérateur
 Nombre de messages : 246 Nombre de messages : 246
Age : 24
Date d'inscription : 27/06/2008
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 22:12 Mar 05 Aoû 2008, 22:12 | |
| - selfrespect a écrit:
- soit (x,y)=(sin(u),cos(u)) avec u decrit [o,Pi/2]
On remarque integ_{o^pi/2}cos(u)f(sin(u))du=integ_{o^1}f(t)dt=integ_{o^pi/2}sin(u)f(cos(u))
alors integronc linegalité entre O et pi/2 On aura : 2integ{O^1}f(t)dt=<pi/2
d'ou integ (O..Pi/2) f(t)dt=<Pi/4. se
cas degalité x--> 1/(1+t²) marche bien je pense.
A+ La démonstration est juste pour yf(x)+xf(y) =1 Pour généraliser sur le cas =< il suffit de poser (x,y)=(µ(u)cos(u),µ(u)sin(u)) avec µ une fonction à valeurs £[0,1]. Le résultat est évident ainsi.
Dernière édition par exodian95 le Mar 05 Aoû 2008, 22:24, édité 3 fois | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 22:16 Mar 05 Aoû 2008, 22:16 | |
| - exodian95 a écrit:
- selfrespect a écrit:
- soit (x,y)=(sin(u),cos(u)) avec u decrit [o,Pi/2]
On remarque integ_{o^pi/2}cos(u)f(sin(u))du=integ_{o^1}f(t)dt=integ_{o^pi/2}sin(u)f(cos(u))
alors integronc linegalité entre O et pi/2 On aura : 2integ{O^1}f(t)dt=<pi/2
d'ou integ (O..Pi/2) f(t)dt=<Pi/4. se
cas degalité x--> 1/(1+t²) marche bien je pense.
A+ La démonstration est juste pour yf(x)+xf(y)=1
Pour généraliser sur le cas =< il suffit de poser (x,y)=(acos(u),asin(u)) avec a£[0,1]. Le résultat est évident ainsi. hmm , non je pense que ce a n'a aucun job içi car en effet x et y se se balançent dans [0,1]² , et c le meme pour cos(U), sin(U).lorsqu u se promene dans [O,Pi/2] .(je ne vois pas pourquoi cette demo est juste seulemnt pr l'egalité? )  | |
|
  | |
exodian95
Modérateur
 Nombre de messages : 246 Nombre de messages : 246
Age : 24
Date d'inscription : 27/06/2008
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 22:22 Mar 05 Aoû 2008, 22:22 | |
| x,y se balancent indépendemment comme il n'y a pas d'égalité. Dsl, j'ai du faire qq changements. | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 22:25 Mar 05 Aoû 2008, 22:25 | |
| - exodian95 a écrit:
- x,y se balancent indépendemment comme il n'y a pas d'égalité. Dsl, j'ai du faire qq changements.
Ah bin , l'inegalité est vrai pour x,y independants ==> elle est vrai pr x, y liées ,!! l'essentiel c'etait d'arriver a exprimer integ_{o^1}f(t)dt . | |
|
  | |
exodian95
Modérateur
 Nombre de messages : 246 Nombre de messages : 246
Age : 24
Date d'inscription : 27/06/2008
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 23:14 Mar 05 Aoû 2008, 23:14 | |
| Dsl, selfrespect. J'ai revu attentivement ta réponse et c'est très bon. Juste que ta rédaction m'a un peu tourmenté.
Continue.
A+ | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 23:26 Mar 05 Aoû 2008, 23:26 | |
| - exodian95 a écrit:
- Dsl, selfrespect. J'ai revu attentivement ta réponse et c'est très bon. Juste que ta rédaction m'a un peu tourmenté.
Continue.
A+ Ok desolé , si ma redaction n'est pas si belle que mon avatar  . A+ | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  Mar 05 Aoû 2008, 23:58 Mar 05 Aoû 2008, 23:58 | |
| oui selresêct c'est la mème réponse que j'ai trouvé,iwa ssahbi t'as pas trouvé aucun avatare que celui ci,il me fait tjr peur,quant à ta rédaction,elle est pertinante saut il serait mieux utiliser mathstype pour bien faire apparaitre les symbole!! | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: exercice )5(: Sujet: Re: exercice )5(:  | |
| |
|
  | |
| | exercice )5(: |  |
|
