| | Un deuxième :Théorème de Liouville,Fermat pour les polynômes |  |
|
|
| Auteur | Message |
|---|
callo
Expert sup

 Nombre de messages : 1481 Nombre de messages : 1481
Age : 34
Localisation : paris
Date d'inscription : 03/03/2007
 |  Sujet: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Sam 16 Mai 2009, 20:50 Sam 16 Mai 2009, 20:50 | |
| Trouver les solutions (d'inconnues A,B et C dans K[X]) de l'equation suivante
A^n +B^n+C^n=0 , n>=3 | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Dim 17 Mai 2009, 14:52 Dim 17 Mai 2009, 14:52 | |
| Salam alikom Hamza  , 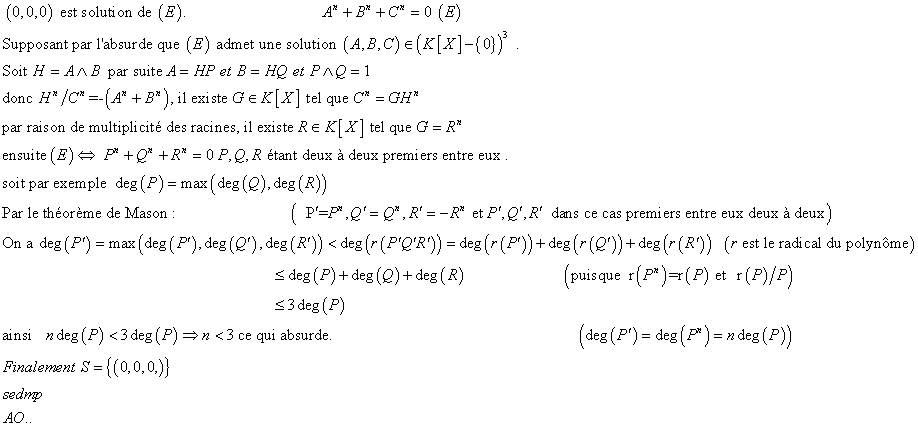 | |
|
  | |
callo
Expert sup

 Nombre de messages : 1481 Nombre de messages : 1481
Age : 34
Localisation : paris
Date d'inscription : 03/03/2007
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Dim 17 Mai 2009, 16:31 Dim 17 Mai 2009, 16:31 | |
| Wa Alikom salam Omar ,
les étapes démonstration sont justes , sauf une toute petite étourderie quant à la conclusion.
La conclusion est que les polynômes sont de degré nul...tq a^n+b^n+c^n=0...exemple A=i B=i C=-2^1/3 * i
... | |
|
  | |
hamzaaa
Expert sup

 Nombre de messages : 744 Nombre de messages : 744
Age : 37
Localisation : Montréal...
Date d'inscription : 15/11/2007
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Dim 17 Mai 2009, 18:12 Dim 17 Mai 2009, 18:12 | |
| Ce théorème de Mason est-il au programme? | |
|
  | |
callo
Expert sup

 Nombre de messages : 1481 Nombre de messages : 1481
Age : 34
Localisation : paris
Date d'inscription : 03/03/2007
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Dim 17 Mai 2009, 19:11 Dim 17 Mai 2009, 19:11 | |
| Il n'est pas au programme,apparemment Omar l'a eu en Ds et Dm ;
Il y a une deuxième preuve du théorème de Liouville, une preuve directe. | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Lun 18 Mai 2009, 01:15 Lun 18 Mai 2009, 01:15 | |
| je pense que l'exo est facile,j'ai trouvé une solution élémentaire on utilisant seulement la derivation,je vais l poster apres inchallah.mais pour l'utilisation d'un grand theoreme comme celui de mason franchement c'est pas favorable sur tt sans le demontrer .(amicalement) | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Lun 18 Mai 2009, 01:41 Lun 18 Mai 2009, 01:41 | |
| - kalm a écrit:
- je pense que l'exo est facile,j'ai trouvé une solution élémentaire on utilisant seulement la derivation,je vais l poster apres inchallah.mais pour l'utilisation d'un grand theoreme comme celui de mason franchement c'est pas favorable sur tt sans le demontrer .(amicalement)
Salam alikom, J'ai su que Hamza connaît ce théorème avant de rédiger ma solution c'est pour ça que je l'ai utilisé en attendant d'autres propositions.. Amicalement | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Lun 18 Mai 2009, 12:44 Lun 18 Mai 2009, 12:44 | |
| autre solution sans utiliser le fameux théorème de MASON.
quitte à diviser par le pgcd de P,Q et R on suppose que pgcd(P,Q,R)=1.on remarque également que P,Q et R sont premiers entre ux deux à deux (pourquoi?).on se ramène donc à montrer que P,Q,R sont des polynomes constantes.
supposons que deg(P)=<deg(Q)=<deg(R).
Si P est une constante alors R^n+Q^n=produc(i=1...n)(R-n_k*Q) l'est aussi avec n_k les racines n-ioème de -1.il vient donc que R-n_k*Q sont ous constantes,ce qui montre en définitive que R et Q sont des Cstes.
mnt il reste à montrer que P est en fait constante.supposons par absurde que deg(P)>=1.
on dérive la relation (E) ==> (E') P^(n-1)*P'+R^(n-1)*R'+Q^(n-1)*Q=0.
en faisant P'*(E)-P*(E')==>Q^(n-1)*(Q'*P-Q*P')=R^(n-1)*(R*P'-R'*P)
en vertu du théorème de GAUSS il vient que R^(n-1) divise Q'*P-Q*P'.
Or Q'*P-Q*P' n'est pas nul (pourquoi?).
(n-1)deg(R)=<max(deg(Q'*P),deg(Q*P'))=deg(Q)+deg(P)+1
=<2deg(P)-1
ce qui est absurde car n>=3.
l'ensemble des solutions de E est donc les triplets (x*P,y*P,z*P) avec x,y et z des complexes vérifiant x^n+y^n+z^n=0.
----------------------------------------------------------
radouane. | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  Lun 18 Mai 2009, 14:03 Lun 18 Mai 2009, 14:03 | |
| ohhh,c'est presque la meme demarche que j'ai suivi,mais j'ai pas fait le meme debut de la solution,donc c'est pas la peine de poster la mienne,bien vu radouan . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes Sujet: Re: Un deuxième :Théorème de Liouville,Fermat pour les polynômes  | |
| |
|
  | |
| | Un deuxième :Théorème de Liouville,Fermat pour les polynômes |  |
|
