| | un petit problème |  |
|
|
| Auteur | Message |
|---|
redeye
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 31
Date d'inscription : 18/08/2009
 |  Sujet: un petit problème Sujet: un petit problème  Mer 19 Aoû 2009, 13:25 Mer 19 Aoû 2009, 13:25 | |
| slt c'est l'un de mes premiers messages sur ce forum passionnant.
je suis un futur élève de 1ab sc math et jé trouvé un petit problème avec cet exo qui se présente comme tel:
a et b sont deux nombres réels puisque:|a|≥1 et |b|≥1
démontrer que: √(1-a^2 )+√(1-b^2 ) ≤ 2√(1-((a+b)/2)^2 )
merci d'avance et désolé pour l'écriture(problème avec latex) | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Mer 19 Aoû 2009, 13:28 Mer 19 Aoû 2009, 13:28 | |
| bonjour redeye et sois la vien venue avec nous dans le forum....ton premeir petit problème est trés beau surtout qu'on peut en trouver plusisuers démos dont l'une utilise un peu de géométrie...mais tt d'abord laissons nous voir les démos des autres et puis on verra ce que va donner Euclide avec sa géométrie! | |
|
  | |
redeye
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 31
Date d'inscription : 18/08/2009
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Mer 19 Aoû 2009, 13:37 Mer 19 Aoû 2009, 13:37 | |
| merci!!
et je suis un mec(mon nom est reda c pour ça que jé choisi le pseuso redeye d'ailleurs je vais changer le pseudo) | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Mer 19 Aoû 2009, 17:09 Mer 19 Aoû 2009, 17:09 | |
| | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Mer 19 Aoû 2009, 17:13 Mer 19 Aoû 2009, 17:13 | |
| premierement je crois que tu veux dire |a|≤1 et |b|≤1 et non pas |a|≥1 et |b|≥1
n'est ce pas? | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Mer 19 Aoû 2009, 17:34 Mer 19 Aoû 2009, 17:34 | |
| wé ta raison c ça désolé pour cette erreur d'inattention | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Jeu 20 Aoû 2009, 00:25 Jeu 20 Aoû 2009, 00:25 | |
| allez les amis je voudrais avoir une réponse plizz | |
|
  | |
paheli
Expert sup

 Nombre de messages : 688 Nombre de messages : 688
Age : 34
Localisation : somewhere
Date d'inscription : 19/08/2007
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Jeu 20 Aoû 2009, 01:27 Jeu 20 Aoû 2009, 01:27 | |
| salam
voici ma solution
enlever le carré deux fois
développer l'expression
factoriser
tu aura (a-b)²≥0
A+Waraq
Dernière édition par paheli le Jeu 20 Aoû 2009, 23:21, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Jeu 20 Aoû 2009, 09:47 Jeu 20 Aoû 2009, 09:47 | |
| bonjour...
je vois qu'aucune méthode n'est postée donc je propose cette solution(sauf erreur)...
commençons par démontrer que pour (x,y)£IR² on a :
(x+y)²≤2(x²+y²) l'inégalité est équivalente à :
x²+y²+2xy≤2(x²+y²) <=>2xy≤x²+y²<=>0≤(x-y)² ce qui tjs vrai
-----------------------------------------------------------------
(x+y)²≤2(x²+y²) --->x+y≤√[2(x²+y²)] (avec x et y positifs)
maintenant remplaçons x par √(1-a²) et y par √(1-b²)
alors on a √(1-a²)+√(1-b²)≤√[2(2-a²-b²)]
<=>√(1-a²)+√(1-b²)≤√(4-2a²-2b²) (1)
on a (x+y)²≤2(x²+y²) <=>-2(x²+y²)≤-(x+y)²
remplaçons x par a et y par b donc ça devient:
2(a²+b²)≤-(a+b)²<=>4-2a²-2b²≤4-(a+b)²
et on a 4-2a²-2b²≥0 et 4-(a+b)²≥0 (car |a|≤1 et |b|≤1)
alors √(4-2a²-2b²)≤√[4-(a+b)²]=2√(1-((a+b)/2)²)
----->√(4-2a²-2b²)≤2√(1-((a+b)/2)²]) (2)
-----------------------------------------------------------------------
de (1) et (2) on a :√(1-a^2 )+√(1-b^2 ) ≤ 2√(1-((a+b)/2)² ) | |
|
  | |
paheli
Expert sup

 Nombre de messages : 688 Nombre de messages : 688
Age : 34
Localisation : somewhere
Date d'inscription : 19/08/2007
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Jeu 20 Aoû 2009, 15:29 Jeu 20 Aoû 2009, 15:29 | |
| Salam 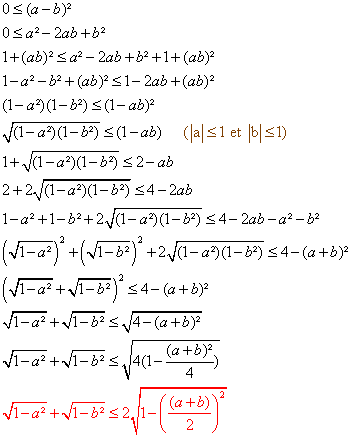 | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 | |
  | |
paheli
Expert sup

 Nombre de messages : 688 Nombre de messages : 688
Age : 34
Localisation : somewhere
Date d'inscription : 19/08/2007
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Jeu 20 Aoû 2009, 19:51 Jeu 20 Aoû 2009, 19:51 | |
| Salam de rien  | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  Jeu 20 Aoû 2009, 21:57 Jeu 20 Aoû 2009, 21:57 | |
| hmmm avez vous pensez à ce changement de variables,x=sin(t) et y=sin(z),lol! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: un petit problème Sujet: Re: un petit problème  | |
| |
|
  | |
| | un petit problème |  |
|
