Même je ne suis pas de ce niveau, j'ai essayé avec cet exercice.
Avant de commencer, je démontre ce que je vais utiliser:
En un premier temps:
On a
^2+(\sin{x}-\cos{x})^2=\sin^2{x}+2\sin{x}*\cos{x}+\cos^2{x}+\sin^2{x}-2\sin{x}*\cos{x}+\cos^2{x})
.
Donc
^2+(\sin{x}-\cos{x})^2=\sin^2{x}+\cos^2{x}+\sin^2{x}+\cos^2{x})
.
Donc
^2+(\sin{x}-\cos{x})^2=1+1)
.
Donc
^2+(\sin{x}-\cos{x})^2=2)
.==>(1)
Posons
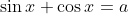
.
On a
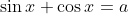
.
Donc
^2=a^2)
.
Donc
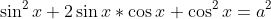
.
Donc
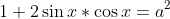
.
Donc
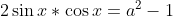
.
Donc
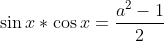
.
D'autre part
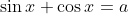
.
Donc
^3=a^3)
.
Donc
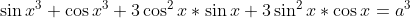
.
Donc
=a^3)
.
Donc
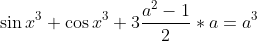
.
Donc
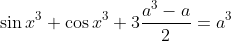
.
Donc
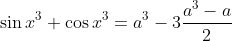
.
Donc
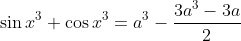
.
Donc
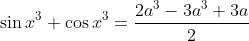
.
Donc
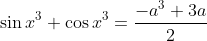
.
Maintenant au travail:
On a
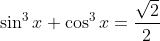
.
Donc
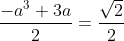
.
Donc
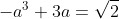
.
Donc
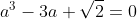
.
Remarquons que

est une racine évidente.
La division euclidienne du polynôme
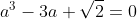
sur
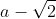
donne le polynôme
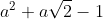
.
On a
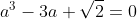
.
Donc
(a^2+a\sqrt{2}-1)=0)
.
Donc
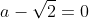
ou
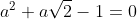
.
Considérons le binôme
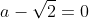
.
Qui s'annule si
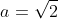
.
Considérons le trinôme
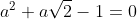
.
Ce trinôme a pour discriminent
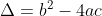
.
Donc
^2-4*1*1)
.
Donc
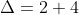
.
Donc
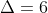
.
Et il a pour solution
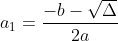
et
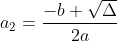
.
Donc
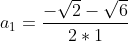
et
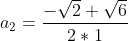
.
Donc
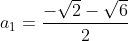
et
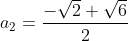
.
On a
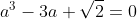
.
Donc
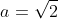
ou
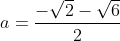
ou
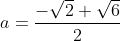
.
Soit
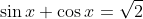
ou
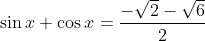
ou
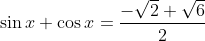
.
====Considérons l'équation
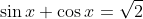
.
Et soit S1 l'ensemble de ses solutions, Utilisons 1:
Et puisque
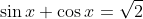
.
Il vient que
^2+(\sqrt{2})^2=2)
.
Donc
^2+2=2)
.
Donc
^2=0)
.
Donc
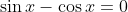
.
On conclut que résoudre en IR l'équation proposé n'est autre que résoudre le système:
\begin{cases}\sin{x}-\cos{x}=0\\\sin{x}+\cos{x}=\sqrt{2}\end{cases})
.
Par addition des lignes, on trouve
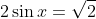
.
Donc
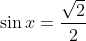
.
Et par la suite
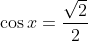
.
Le tableau des rapports usuels affirme que
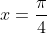
.
D'ou finalement
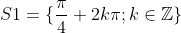
.
====Considérons l'équation
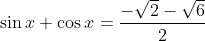
.
Et soit S2 l'ensemble de ses solutions, Utilisons 1:
Et puisque
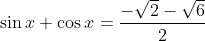
.
Il vient que
^2+(\frac{-\sqrt{2}-\sqrt{6}}{2}})^2=2)
.
Donc
^2+(\frac{\sqrt{2}+\sqrt{6}}{2}})^2=2)
.
Donc
^2+\frac{6+2\sqrt{12}+2}{4}=2)
.
Donc
^2+\frac{8+4\sqrt{3}}{4}=2)
.
Donc
^2+2+\sqrt{3}=2)
.
Donc
^2+\sqrt{3}=0)
.
Donc
^2=-\sqrt{3})
.
Donc S2 est l'ensemble vide.
====Considérons l'équation
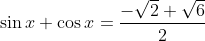
.
Et soit S3 l'ensemble de ses solutions, Utilisons 1:
Et puisque
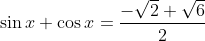
.
Il vient que
^2+(\frac{-\sqrt{2}+\sqrt{6}}{2}})^2=2)
.
Donc
^2+\frac{6-2\sqrt{12}+2}{4}=2)
.
Donc
^2+\frac{8-4\sqrt{3}}{4}=2)
.
Donc
^2+2-\sqrt{3}=2)
.
Donc
^2-\sqrt{3}=0)
.
Donc
^2=\sqrt{3})
.
Donc
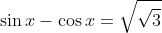
ou
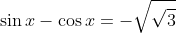
.
On conclut que résoudre en IR l'équation proposé n'est autre que résoudre les deux systèmes:
\begin{cases}\sin{x}-\cos{x}=\sqrt{\sqrt{3}}\\\sin{x}+\cos{x}=\frac{-\sqrt{2}+\sqrt{6}}{2}\end{cases})
et
\begin{cases}\sin{x}-\cos{x}=-\sqrt{\sqrt{3}}\\\sin{x}+\cos{x}=\frac{-\sqrt{2}+\sqrt{6}}{2}\end{cases})
.
==Commençons par le système S.
Par addition des lignes, on trouve
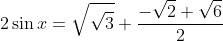
.
Donc
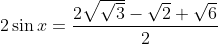
.
Donc
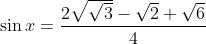
.
Et par la suite
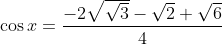
.
Par une calculatrice, on obtient
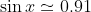
et
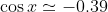
.
Soit

.
==Maintenant le système S'.
Par addition des lignes, on trouve
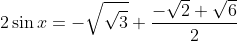
.
Donc
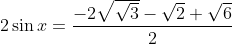
.
Donc
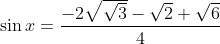
.
Et par la suite
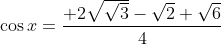
.
Par une calculatrice, on obtient
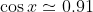
et
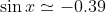
.
Soit

.
Soit finalement

.
La solution du système proposé au début est l'intersection de S1, S2, et S3.
Sauf erreur.
J'attends vos confirmation.
